Exo 5
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
l'endomorphisme de
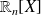défini par :
.
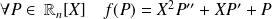Question
Déterminer la matrice de
dans la base canonique de
.
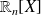En déduire que l'application
est un automorphisme de
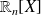et déterminer son application réciproque.
Déterminez le polynôme
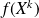pour tout
.
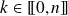La linéarité de
a été démontrée dans l'exercice
.
La base canonique de
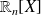est
.
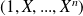Pour tout
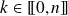, si
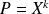, alors
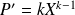et
.
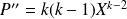Donc :
.
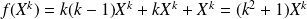Donc l'image de la base canonique de
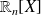est
,
,
, ...,
.
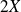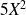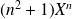La matrice de
a pour
ème colonne les coefficients de
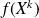dans la base
.
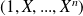Conclusion : La matrice de
est la matrice
.
C'est une matrice diagonale sans zéros sur la diagonale. Donc elle est inversible.
Conclusion : L'application
est un automorphisme de
.
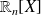L'application réciproque
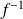a pour matrice
.
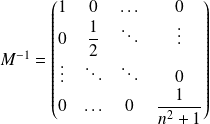Si
, donc si
a pour matrice
, alors
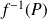a pour matrice
.
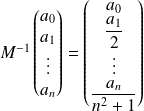Conclusion : Si
, alors
.
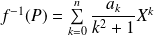Remarque : Remarque
On aurait pu montrer directement que l'application
est bijective.
En effet, si
, alors par linéarité
.
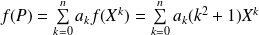Soit
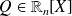tel que
.
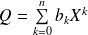Alors
si et seulement si
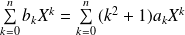, donc si
par unicité des coefficients.
Donc l'équation
a une unique solution
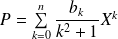. Donc l'application
est bijective.
