Exo 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère la matrice
.
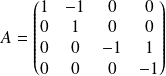Question
Calculer
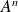pour tout entier naturel
non nul.
Indice
Décomposez la matrice
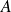en somme de deux matrices qui commutent et dont les puissances sont faciles à calculer, puis utilisez la formule du binôme.
Solution
On peut remarquer que
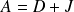en posant :
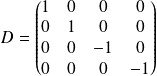et
.
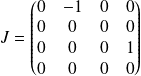Or :
.
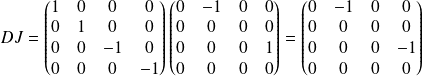Et :
.
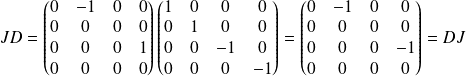Donc les matrices
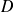et
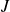commutent.
Donc, d'après la formule du binôme :
.
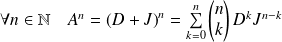Or
.
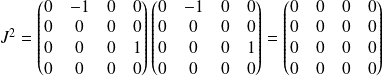Donc :
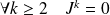. Donc :
.
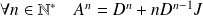Donc :
.
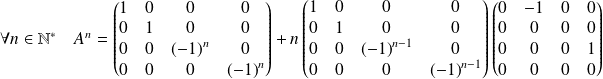Conclusion :
.
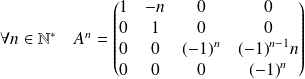