Opérations sur les matrices
Définition :
Addition de deux matrices :
Si
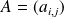et
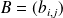appartiennent à
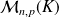, la matrice
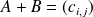appartient à
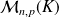et est définie par :
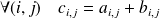.Multiplication d'une matrice par un scalaire :
Si
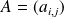appartient à
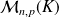et
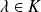, la matrice
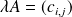appartient à
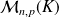et est définie par :
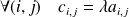.Produit de deux matrices :
Si
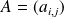appartient à
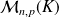et
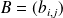appartient à
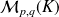, la matrice
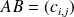appartient à
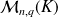et est définie par :
.
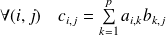Pour additionner deux matrices (de mêmes dimensions), on additionne les éléments terme à terme.
Pour multiplier une matrice par un scalaire, on multiplie tous les termes par ce scalaire.
Lorsque l'on multiplie deux matrices, le terme
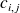est obtenu en "multipliant" la ligne
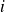de la première matrice par la colonne
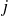de la deuxième matrice.
Exemple :
.
.
.
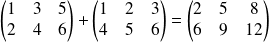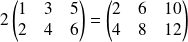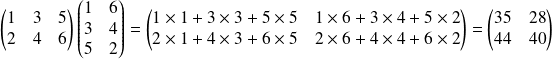Fondamental :
Propriétés :
-
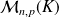muni de l'addition et de la multiplication par un scalaire est un espace vectoriel de dimension
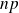. La multiplication des matrices est associative, distributive à gauche et à droite par rapport à l'addition, non commutative.
.
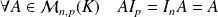Attention :
Tous les produits de matrices ne sont pas définis. Il faut que les dimensions soient compatibles.
La multiplication des matrices n'est pas commutative.
Exemple :
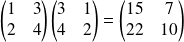et
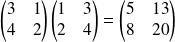.On dira que deux matrices
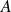et
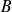commutent si
.
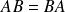Un produit de deux matrices peut être nul sans qu'aucune des deux ne le soit.
Exemple :
.
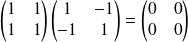Fondamental :
Formule du binôme de Newton :
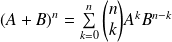si les matrices
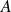et
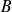commutent.
Définition :
Si un polynôme
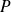est défini par
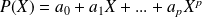, alors à toute matrice
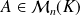, on associe la matrice :
.
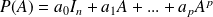