Exo 12
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Un avare compte ses pièces d'or
Il lui en reste toujours une. Il les compte
|  |
Question
Combien a-t-il de pièces au minimum?
Traduisez les hypothèses en termes de divisibilité, et ramenez vous à la résolution d'une identité de Bezout.
Le nombre
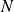de pièces est un multiple de
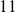. Donc il existe
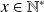tel que :
.
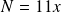Et
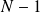est divisible par
,
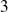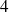et
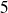, qui sont premiers entre eux.
Donc
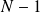est divisible par
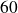. Donc il existe
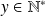tel que :
.
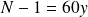Donc :
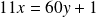. Or :
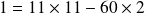. Donc :
.
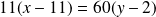Donc
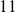divise
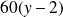et
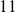est premier avec
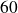. Donc
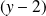est divisible par
.
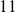Donc il existe
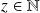tel que
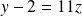. Donc :
.
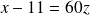Donc :
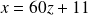et
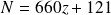avec
.
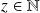Conclusion : L'avare a au moins
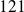pièces d'or.
