Exo 11
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions suivantes sont indépendantes.
Question
Résoudre l'équation
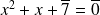 dans
dans
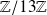 .
.
Factorisez le premier membre et remarquez que
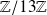 est un corps.
est un corps.
Dans
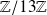 , l'équation équivaut à :
, l'équation équivaut à :
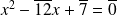 , donc à :
, donc à :
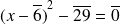 .
.
Or dans
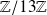 :
:
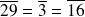 . Donc l'équation équivaut à :
. Donc l'équation équivaut à :
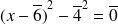 .
.
Donc l'équation équivaut à
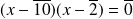 .
.
Or
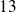 est un nombre premier, donc
est un nombre premier, donc
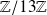 est un corps, donc est intègre.
est un corps, donc est intègre.
Conclusion : Les solutions de l'équation sont
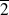 et
et
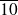 .
.
Question
Résoudre l'équation
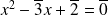 dans
dans
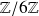 .
.
Factorisez le premier membre et déterminez les diviseurs de
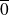 .
.
Dans
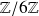 , l'équation équivaut à :
, l'équation équivaut à :
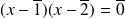 .
.
Donc
 et
et
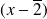 sont des diviseurs de
sont des diviseurs de
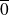 .
.
Or
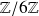 n'est pas un anneau intègre car
n'est pas un anneau intègre car
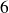 n'est pas un nombre premier.
n'est pas un nombre premier.
Les diviseurs de
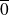 sont :
sont :
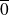 ,
,
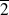 ,
,
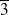 et
et
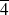 .
.
On obtient donc :
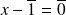 ou
ou
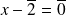 ou
ou
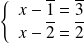 ou
ou
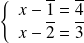 .
.
Conclusion : Les solutions de l'équation sont
 ,
,
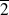 ,
,
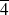 et
et
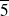 .
.
Question
Soient
 et
et
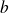 deux éléments de
deux éléments de
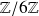 .
.
Dans
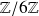 , résoudre, suivant les valeurs de
, résoudre, suivant les valeurs de
 et
et
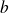 , le système :
, le système :
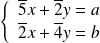 .
.
Remarquez que pour qu'il y ait des solutions, il faut que
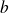 soit multiple de
soit multiple de
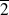 .
.
On peut d'abord remarquer que la deuxième équation implique que
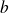 soit un multiple de
soit un multiple de
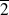 .
.
Or, dans
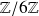 , les multiples de
, les multiples de
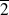 sont :
sont :
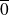 ,
,
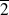 et
et
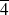 .
.
Donc si
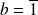 ou
ou
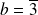 ou
ou
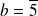 , le système n'a pas de solution.
, le système n'a pas de solution.
En additionnant membre à membre, le système équivaut à :
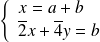 .
.
Donc il équivaut à :
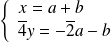 , donc à :
, donc à :
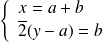 .
.
Si
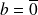 , on obtient :
, on obtient :
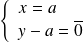 ou
ou
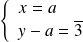 , donc :
, donc :
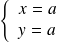 ou
ou
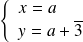 .
.
Si
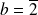 , on obtient :
, on obtient :
 ou
ou
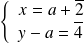 , donc :
, donc :
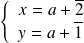 ou
ou
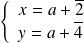 .
.
Si
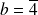 , on obtient :
, on obtient :
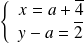 ou
ou
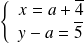 , donc :
, donc :
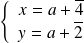 ou
ou
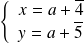 .
.
Conclusion :
Si
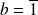 ,
,
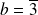 ou
ou
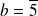 , le système n'a pas de solution.
, le système n'a pas de solution.Si
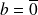 , les solutions sont :
, les solutions sont :
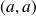 et
et
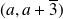 .
.Si
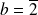 , les solutions sont :
, les solutions sont :
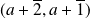 et
et
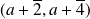 .
.Si
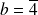 , les solutions sont :
, les solutions sont :
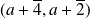 et
et
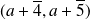 .
.





