Congruence modulo n
Définition :
Si
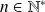, un entier
est congru à un entier
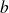modulo
si
divise
.
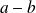On note :
.
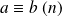Fondamental :
Propriétés :
Si
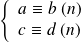, alors
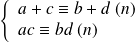.Si
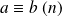, alors
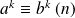pour tout
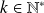.Si
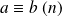, alors
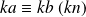pour tout
.
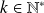Définition :
La relation de congruence modulo
est une relation d'équivalence sur
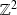compatible avec l'addition et la multiplication.
L'ensemble quotient est noté
.
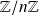Fondamental :
Propriétés :
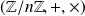est un anneau commutatif. Le nombre d'éléments inversibles de cet anneau est :
.-
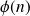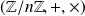est un corps si et seulement si
est premier.
Fondamental :
Petit théorème de Fermat :
Si
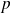est premier :
.
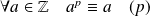Fondamental :
Théorème des restes chinois :
Si
, ...,
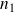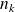sont des entiers naturels
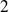à
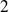premiers entre eux, alors pour tous les entiers
, ...,
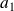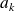, il existe un entier
tel que :
.
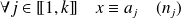Cet entier
est unique modulo
.
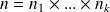