Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Montrer qu'il y a une infinité de nombres premiers de la forme
.
Raisonnez par l'absurde.
Soit
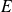l'ensemble des nombres premiers de la forme
. Il n'est pas vide puisque
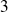appartient à
.
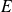On raisonne par l'absurde en supposant que
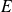est un ensemble fini de cardinal
.
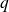Donc, on peut noter :
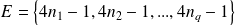avec
.
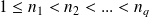Soit :
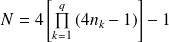et
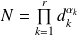sa décomposition en facteurs premiers.
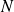est un entier impair, donc tous les
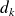sont impairs, donc de la forme
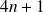ou
.
Or pour tous les entiers
et
:
.
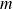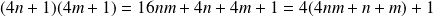Donc si tous les
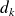étaient de la forme
,
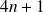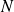serait aussi de la forme
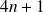, ce qui est faux.
Donc l'un au moins des
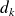est de la forme
, donc appartient à
:
.
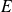Donc
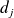divise
et
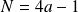. Donc
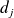divise
. Or
.
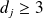On aboutit donc à une contradiction. Donc
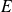n'est pas un ensemble fini.
Conclusion : Il y a une infinité de nombres premiers de la forme
.
