Nombres premiers
Définition :
Un entier
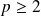est premier si :
.
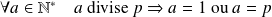L'ensemble des nombres premiers est infini.
Fondamental :
Propriétés :
Si
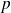est premier :
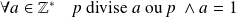.Si
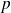est premier :
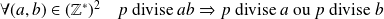.Si
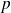et
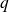sont premiers et
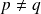, alors
.
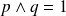Fondamental :
Décomposition en facteurs premiers :
Tout entier
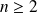se décompose de manière unique sous la forme
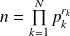où
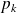est premier et
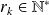pour tout
.
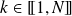L'unicité est vraie à l'ordre près des
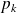puisque la multiplication est commutative.
Fondamental :
Conséquences :
Si
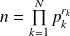, alors
.
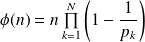Si
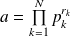et
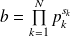, alors :
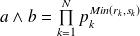et
.
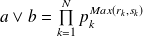Pour tous
,
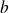et
entiers non nuls :
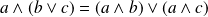.Pour tous
,
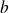et
entiers non nuls :
.
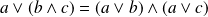