Exo 9
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
et
deux entiers supérieurs ou égaux à
.
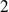Question
Démontrer que si
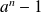est un nombre premier, alors
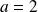et
est un nombre premier.
Pour démontrer que
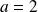, factorisez
.
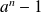Pour démontrer que
est un nombre premier, raisonnez par l'absurde.
On factorise :
. Donc
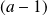est un diviseur de
.
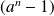Or
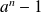est premier, donc il n'admet comme diviseurs que
et lui-même.
Or
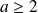, donc
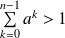. Donc
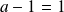. Donc :
.
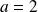Montrons que
est un nombre premier en raisonnant par l'absurde.
Supposons que
n'est pas premier. Donc
admet un diviseur
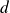différent de
et de
.
Donc
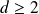et il existe un entier
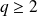tel que
.
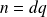Donc :
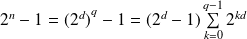. Donc
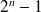admet un diviseur
.
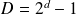Or
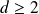, donc
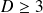, donc
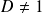. Et
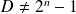car
.
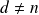Donc, on aboutit à une contradiction car
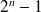est premier.
Conclusion : Si
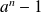est un nombre premier, alors
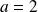et
est un nombre premier.
Question
Démontrer que si
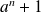est un nombre premier, alors
est une puissance de
.
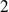Démontrez d'abord que
est pair, puis utilisez sa décomposition en facteurs premiers.
Montrons d'abord que
est pair en raisonnant par l'absurde.
Supposons que
est impair. Donc il existe un entier
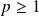tel que :
.
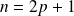Donc :
.
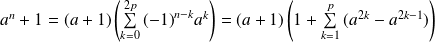Or
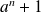est premier, donc il n'admet comme diviseurs que
et lui-même.
Or, comme
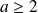, alors :
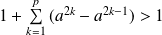, et
.
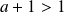On aboutit donc à une contradiction. Donc l'entier
est pair.
Soit
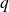la puissance du diviseur premier
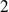dans sa décomposition en facteurs premiers.
Les autres facteurs premiers sont impairs. Donc il existe un entier
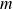impair tel que :
.
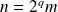Donc :
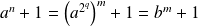en posant
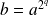. Or
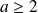, donc
.
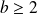Or on a montré que si
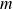est impair et
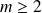, alors
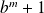n'est pas un nombre premier.
Or
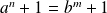est premier. Donc :
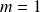. Donc :
.
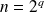Conclusion : Si
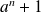est un nombre premier, alors
est une puissance de
.
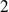