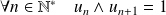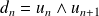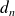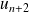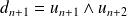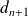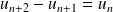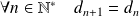Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère la suite de Fibonacci définie par :
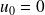 ,
,
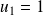 et
et
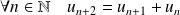 .
.
Question
Question
Démontrer que :
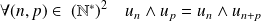 .
.
Démontrez qu'il existe des réels
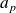 et
et
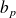 :
:
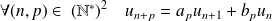 .
.
Pour tout entier
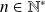 :
:
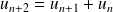 ,
,
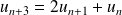 ,
,
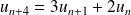 , ...
, ...
Par récurrence double, montrons que, pour tout
 , il existe deux réels
, il existe deux réels
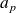 et
et
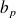 tels que
tels que
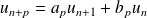 .
.
Initialisation :
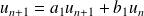 avec
avec
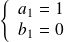 et
et
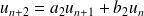 avec
avec
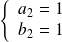 .
.
Hérédité : Soit
 tel que :
tel que :
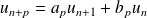 et
et
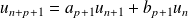 .
.
Donc :
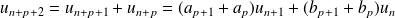 .
.
Donc :
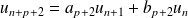 avec :
avec :
 .
.
Conclusion : Pour tout
 , il existe
, il existe
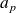 et
et
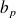 tels que
tels que
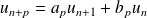 .
.
Les suites
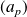 et
et
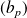 vérifient :
vérifient :
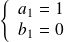 ,
,
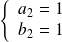 et
et
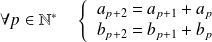 .
.
On retrouve la relation de récurrence de la suite de Fibinacci.
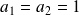 et
et
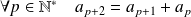 . Donc :
. Donc :
 .
.
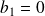 ,
,
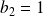 et
et
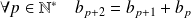 . Donc :
. Donc :
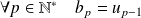 .
.
Donc :
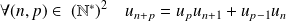 .
.
Donc
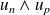 divise
divise
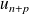 et
et
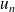 , donc
, donc
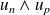 divise
divise
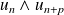 .
.
Et inversement,
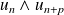 divise
divise
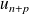 et
et
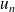 , donc divise
, donc divise
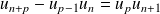 .
.
Or
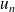 et
et
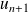 sont premiers entre eux, donc tout diviseur de
sont premiers entre eux, donc tout diviseur de
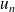 est premier avec
est premier avec
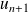 .
.
Donc d'après le théorème de Gauss,
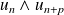 divise
divise
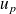 .
.
Donc
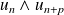 divise
divise
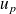 et
et
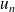 , donc
, donc
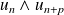 divise
divise
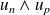 .
.
Conclusion :
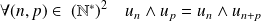 .
.
Question
Démontrer que :
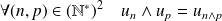 .
.
Si
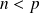 , effectuez la division de
, effectuez la division de
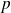 par
par
 et utilisez l'algorithme d'Euclide.
et utilisez l'algorithme d'Euclide.
Soit
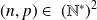 . La relation à démontrer est symétrique entre
. La relation à démontrer est symétrique entre
 et
et
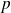 , et elle est évidente si
, et elle est évidente si
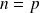 .
.
Donc on peut supposer dans la suite que
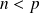 .
.
On divise
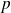 par
par
 : il existe
: il existe
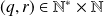 tel que
tel que
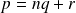 avec
avec
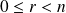 .
.
Si
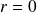 :
:
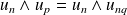 .
. Or, d'après la question précédente :
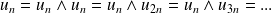
Une récurrence évidente montre que :
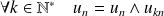 .
.Donc si
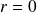 , alors
, alors
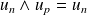 , donc
, donc
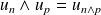 .
.
Si
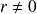 :
:
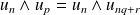 .
. Or, d'après la question précédente :
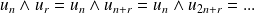
Une récurrence évidente montre que :
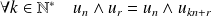 .
.Donc si
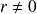 :
:
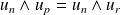 .
. On utilise l'algorithme d'Euclide sur
 et
et
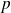 .
.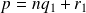 donc
donc
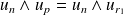 si
si
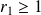 .
.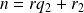 donc
donc
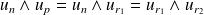 si
si
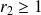 .
.
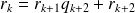 , donc
, donc
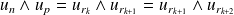 si
si
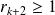 .
.
On continue ainsi jusqu'au dernier reste non nul qui est
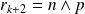 .
. La division suivante donne :
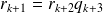 . Donc :
. Donc :
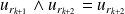 car le reste est nul.
car le reste est nul.Donc :
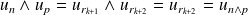 .
.
Conclusion :
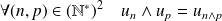 .
.
Remarque :
Une autre solution est possible.
D'après ce qui précède :
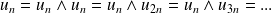
Donc si
 divise
divise
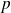 , alors :
, alors :
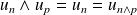 . De même si
. De même si
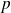 divise
divise
 :
:
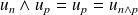 .
.
Dans les autres cas,
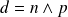 est distinct de
est distinct de
 et de
et de
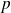 .
.
Et il existe des entiers relatifs non nuls
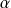 et
et
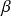 tels que :
tels que :
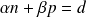 .
.
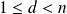 et
et
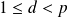 . Donc
. Donc
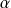 et
et
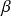 ne peuvent pas être tous les deux positifs, ni tous les deux négatifs.
ne peuvent pas être tous les deux positifs, ni tous les deux négatifs.
Donc l'un est positif et l'autre est négatif. Or
 et
et
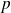 jouent des rôles symétriques, donc on peut supposer
jouent des rôles symétriques, donc on peut supposer
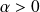 et
et
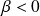 .
.
Donc il existe des entiers naturels
 et
et
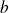 non nuls tels que :
non nuls tels que :
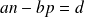 .
.
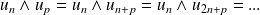 Donc, par récurrence :
Donc, par récurrence :
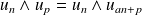 .
.
Donc :
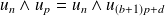 . Or :
. Or :
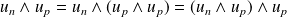 .
.
Donc :
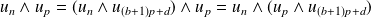 .
.
Or
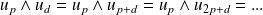 Donc, par récurrence :
Donc, par récurrence :
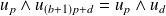 .
.
Or
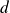 divise
divise
 et
et
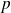 . Donc :
. Donc :
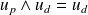 et
et
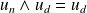 . Donc :
. Donc :
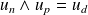 .
.
Conclusion :
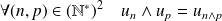 .
.