Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On appelle nombres de Fermat les entiers de la forme
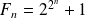 pour
pour
 .
.
Question
Démontrer que
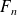 et
et
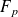 sont premiers entre eux pour tous les entiers
sont premiers entre eux pour tous les entiers
 et
et
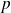 distincts.
distincts.
Exprimez
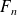 en fonction de
en fonction de
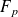 .
.
Soient
 et
et
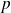 deux entiers naturels tels que
deux entiers naturels tels que
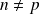 .
.
La propriété à démontrer est symétrique entre
 et
et
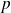 , donc on peut supposer
, donc on peut supposer
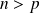 .
.
Donc :
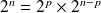 . Donc :
. Donc :
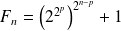 . Donc :
. Donc :
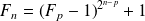 .
.
Donc :
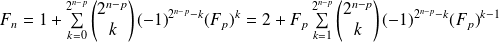 .
.
Donc le PGCD de
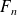 et
et
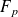 divise
divise
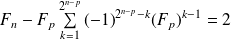 .
.
Donc :
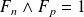 ou
ou
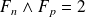 . Or
. Or
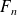 et
et
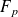 sont impairs. Donc :
sont impairs. Donc :
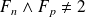 .
.
Conclusion : Si
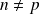 , alors
, alors
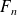 et
et
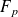 sont premiers entre eux.
sont premiers entre eux.





