Nombres premiers entre eux
Définition :
Deux entiers
et
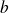sont premiers entre eux si
.
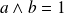Fondamental :
Théorème de Bezout :
Deux entiers
et
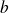sont premiers entre eux si et seulement si il existe
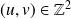tels que
.
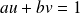Fondamental :
Théorème de Gauss :
Si
divise
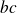et si
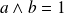, alors
divise
.
Fondamental :
Autres propriétés :
Si
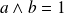et
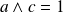, alors
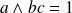.Si
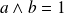, alors
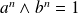pour tout entier naturel
.Si
et
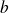divisent
et
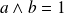, alors
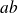divise
.
Définition :
L'indicatrice d'Euler est l'application
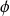définie par :
.
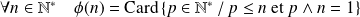Propriété :
.
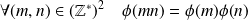Définition :
Pour tout entier
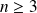, les entiers
,
, ...,
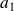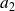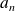sont premiers entre eux dans leur ensemble si leur PGCD est égal à
.
Attention :
Des nombres premiers entre eux dans leur ensemble ne sont pas nécessairement premiers entre eux deux à deux.
