Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
 ,
,
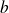 et
et
 trois entiers naturels non nuls. On note
trois entiers naturels non nuls. On note
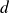 leur PGCD et
leur PGCD et
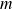 leur PPCM.
leur PPCM.
Question
Montrer que
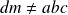 lorsque
lorsque
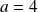 ,
,
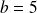 et
et
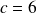 .
.
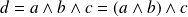 . Or :
. Or :
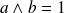 . Donc :
. Donc :
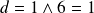 .
.
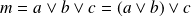 . Or :
. Or :
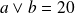 . Donc :
. Donc :
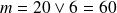 .
.
Donc :
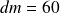 et
et
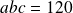 .
.
Conclusion :
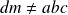 lorsque
lorsque
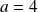 ,
,
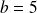 et
et
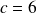 .
.
Remarque :
Pour deux entiers, le produit de leur PGCD et de leur PPCM est égal au produit des deux entiers.
L'exemple précédent montre que c'est faux pour trois entiers.
Par contre, il existe des cas où la propriété est vraie.
Par exemple, si
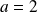 ,
,
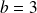 et
et
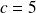 , on a
, on a
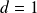 et
et
 , donc :
, donc :
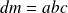 .
.
Question
A quelle condition sur
 ,
,
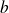 et
et
 a-t-on
a-t-on
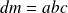 ?
?
Introduisez le PGCD et le PPCM de
 et de
et de
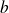 , et utilisez les propriétés démontrées pour deux nombres.
, et utilisez les propriétés démontrées pour deux nombres.
Soit
 ,
,
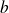 et
et
 tels que
tels que
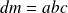 et soit
et soit
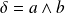 .
.
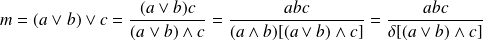 .
.
Donc
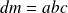 si et seulement si
si et seulement si
 . Or
. Or
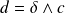 .
.
Donc
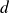 est un diviseur de
est un diviseur de
 , donc
, donc
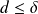 . Donc il faut que :
. Donc il faut que :
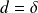 et
et
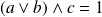 .
.
Or
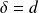 est un diviseur de
est un diviseur de
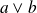 et
et
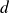 est un diviseur de
est un diviseur de
 . Donc
. Donc
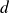 est un diviseur de
est un diviseur de
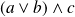 .
.
Donc il faut que
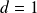 . Or :
. Or :
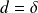 . Donc si
. Donc si
 ,
,
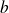 et
et
 sont tels que
sont tels que
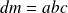 , alors :
, alors :
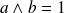 .
.
Les trois entiers
 ,
,
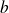 et
et
 jouent des rôles symétriques. Donc :
jouent des rôles symétriques. Donc :
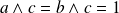 .
.
Réciproquement, on suppose que :
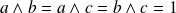 .
.
Donc :
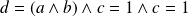 . Et :
. Et :
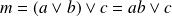 .
.
Or
 est premier avec
est premier avec
 et avec
et avec
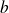 , donc il est premier avec
, donc il est premier avec
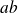 .
.
Donc :
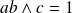 . Donc :
. Donc :
 . Donc :
. Donc :
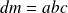 .
.
Conclusion : On a
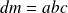 si et seulement si :
si et seulement si :
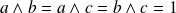 .
.
Remarque :
Le premier exemple montre que la condition
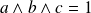 est insuffisante.
est insuffisante.





