PPCM (Plus Petit Commun Multiple)
Si
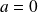ou
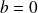, alors
.
Pour tous les entiers
et
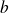non nuls, l'ensemble
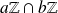est un idéal de
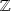non réduit à
.
Définition :
Le PPCM de deux entiers
et
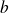non nuls est l'unique entier
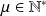tel que
.
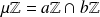On le note :
.
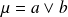Fondamental :
Propriétés :
Deux entiers
et
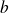non nuls divisent un entier
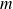si et seulement si
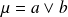divise
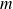.Pour tous
,
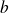et
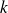entiers non nuls :
.Pour tous
et
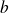entiers non nuls :
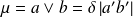si
,
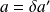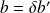et
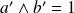(donc si
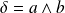).Pour tous
et
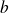entiers non nuls :
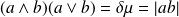.Pour tous
,
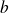et
entiers non nuls :
.
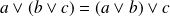Définition :
On définit le PPCM de
entiers par récurrence.
Pour tout entier
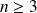et tous les entiers
,
, ...,
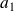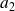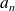non nuls :
.
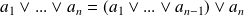