Exo 1
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
 ,
,
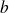 et
et
 trois entiers naturels.
trois entiers naturels.
Question
Montrer que si
 ,
,
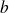 et
et
 ne sont pas multiples de
ne sont pas multiples de
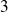 , alors
, alors
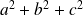 est un multiple de
est un multiple de
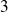 .
.
Etudiez les restes des divisions de
 ,
,
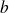 et
et
 par
par
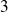 .
.
On effectue les divisions de
 ,
,
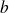 et
et
 par
par
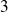 :
:
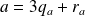 avec
avec
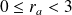 . Or
. Or
 n'est pas multiple de
n'est pas multiple de
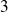 , donc
, donc
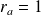 ou
ou
 .
.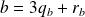 avec
avec
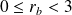 . Or
. Or
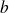 n'est pas multiple de
n'est pas multiple de
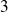 , donc
, donc
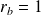 ou
ou
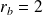 .
.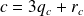 avec
avec
 . Or
. Or
 n'est pas multiple de
n'est pas multiple de
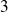 , donc
, donc
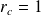 ou
ou
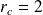 .
.
Donc :
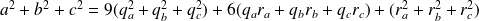 .
.
Les deux premiers termes sont multiples de
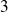 . Etudions le troisième :
. Etudions le troisième :
Si
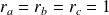 , alors :
, alors :
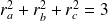 .
.Si
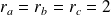 , alors :
, alors :
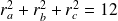 .
.Si deux restes parmi
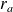 ,
,
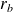 et
et
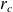 sont égaux à
sont égaux à
 et le troisième à
et le troisième à
 , alors :
, alors :
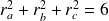 .
.Si deux restes parmi
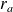 ,
,
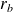 et
et
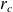 sont égaux à
sont égaux à
 et le troisième à
et le troisième à
 , alors :
, alors :
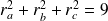 .
.
Donc dans tous les cas,
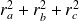 est un multiple de
est un multiple de
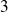 .
.
Conclusion : Si
 ,
,
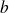 et
et
 sont des entiers naturels qui ne sont pas multiples de
sont des entiers naturels qui ne sont pas multiples de
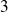 , alors
, alors
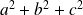 est un multiple de
est un multiple de
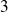 .
.
Question
Montrer que si
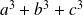 est un multiple de
est un multiple de
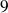 , alors l'un au moins des entiers
, alors l'un au moins des entiers
 ,
,
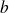 et
et
 est multiple de
est multiple de
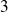 .
.
Démontrez que si
 ,
,
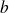 et
et
 ne sont pas multiples de
ne sont pas multiples de
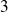 , alors
, alors
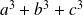 n'est pas un multiple de
n'est pas un multiple de
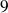 .
.
Par contraposée, c'est équivalent à démontrer que si
 ,
,
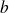 et
et
 ne sont pas multiples de
ne sont pas multiples de
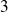 , alors
, alors
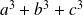 n'est pas un multiple de
n'est pas un multiple de
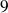 .
.
On reprend les notations précédentes. Donc :
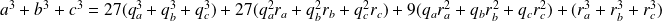 .
.
Les trois premiers termes sont multiples de
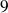 . Etudions le dernier :
. Etudions le dernier :
Si
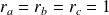 , alors
, alors
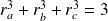 .
.Si
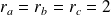 , alors
, alors
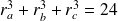 .
.Si deux restes parmi
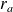 ,
,
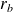 et
et
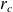 sont égaux à
sont égaux à
 et le troisième à
et le troisième à
 , alors
, alors
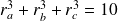 .
.Si deux restes parmi
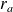 ,
,
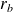 et
et
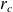 sont égaux à
sont égaux à
 et le troisième à
et le troisième à
 , alors
, alors
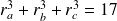 .
.
Donc
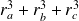 n'est multiple de
n'est multiple de
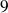 dans aucun des cas.
dans aucun des cas.
Donc si
 ,
,
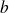 et
et
 ne sont pas multiples de
ne sont pas multiples de
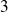 , alors
, alors
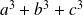 n'est pas un multiple de
n'est pas un multiple de
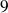 .
.
Conclusion : Si
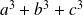 est un multiple de
est un multiple de
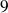 , alors l'un au moins des entiers
, alors l'un au moins des entiers
 ,
,
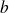 et
et
 est multiple de
est multiple de
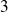 .
.





