Division euclidienne
Définition :
Division euclidienne dans N :
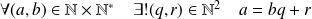 et
et
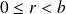 .
.
Définition :
Division euclidienne dans Z :
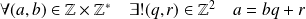 et
et
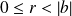 .
.
 est divisible par
est divisible par
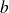 , ou
, ou
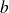 divise
divise
 (noté
(noté
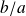 ), ou
), ou
 est un multiple de
est un multiple de
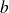 , ou
, ou
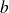 est un diviseur de
est un diviseur de
 s'il existe
s'il existe
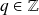 tel que
tel que
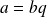 .
.
Fondamental :
Propriétés :
Si
 divise
divise
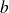 et si
et si
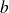 divise
divise
 , alors
, alors
 divise
divise
 .
.Si
 divise
divise
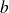 et si
et si
 divise
divise
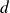 , alors
, alors
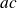 divise
divise
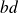 .
.Si
 divise
divise
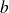 , alors
, alors
 divise
divise
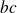 .
.Si
 divise
divise
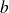 et si
et si
 divise
divise
 , alors
, alors
 divise
divise
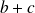 .
.Si
 divise
divise
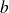 , alors
, alors
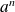 divise
divise
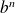 pour tout entier naturel
pour tout entier naturel
 .
.





