Exo 5
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Soit
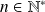. Montrer qu'il existe un unique polynôme
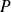(que l'on déterminera) qui vérifie :
.
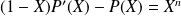Commencez par déterminer le degré du polynôme, puis calculez
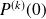et utilisez la formule de Taylor.
Remarquons d'abord que les polynômes constants ne sont pas solutions.
Soit
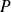un polynôme solution. Soit
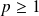son degré et
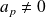son coefficient dominant.
Donc
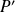est de degré
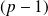et son coefficient dominant est
.
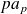Donc
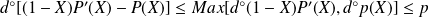et le coefficient de
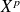dans
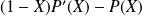est
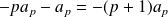, donc non nul.
Donc si
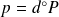, alors
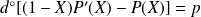. Or :
.
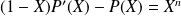Donc si un polynôme
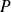est solution, alors
.
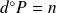En dérivant
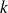fois l'équation
:
.
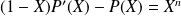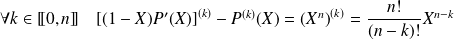D'après la formule de Leibniz :
.
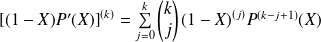Donc :
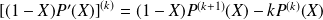si
.
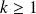Donc :
.
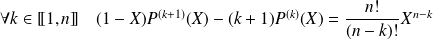Donc :
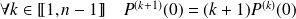et :
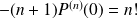car
.
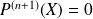De plus
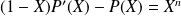. Donc
.
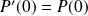Donc :
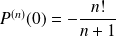et
.
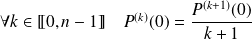Donc :
,
, ...
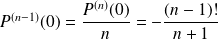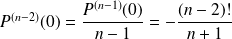Une récurrence évidente montre que :
.
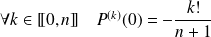Or d'après la formule de Taylor :
.
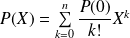Conclusion : L'équation a une unique solution
.
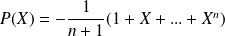