Dérivation
Définition :
Le polynôme dérivé de
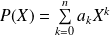est le polynôme :
.
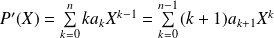Pour tout entier
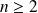, le polynôme dérivé d'ordre
de
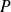, noté
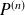, est le polynôme dérivé de
.
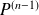Fondamental :
Propriétés :
Si
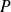est un polynôme de degré
:
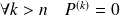.Formule de Taylor :
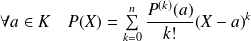si
.
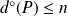Fondamental :
Pour tous polynômes
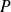et
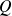, pour tout scalaire
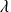et pour tout entier
:
.
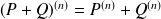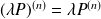.Formule de Leibniz :
.
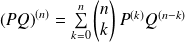