Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Deux parties
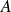et
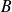non vides de
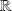sont dites adjacentes si :
.
.
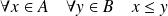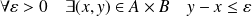Question
Démontrer que si
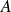et
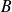sont deux parties adjacentes de
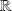, alors
.
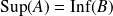Démontrez d'abord que
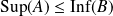, puis raisonnez par l'absurde.
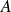est une partie non vide de
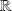majorée par tout élément de
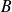. Donc la partie
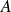possède une borne supérieure
dans
.
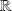Tout élément de
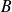majore
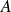et
est le plus petit des majorants de
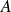, donc :
.
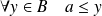De même,
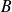est une partie non vide de
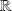minorée par tout élément de
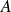. Donc la partie
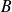possède une borne inférieure
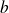dans
.
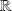Tout élément de
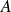minore
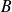et
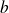est le plus grand des minorants de
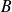, donc :
.
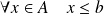Donc
est un minorant de
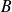et
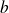est un majorant de
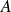. Donc
.
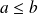Pour montrer que
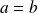, on raisonne par l'absurde.
Supposons que
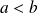et posons
.
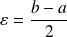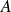et
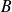sont adjacentes, donc il existe
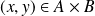tel que :
.
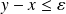Or
majore
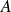et
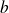minore
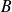. Donc :
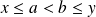. Donc :
.
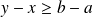Donc :
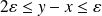, ce qui est faux car
.
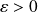Donc l'hypothèse est fausse, et donc :
.
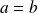Conclusion : Si
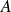et
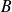sont deux parties adjacentes de
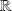, alors
.
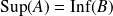Question
Démontrer que
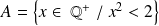et
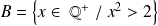sont deux parties adjacentes de
.
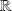Pour tout entier
, introduisez l'ensemble
.
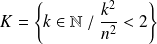Et démontrez qu'il existe
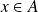et
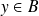tels que
.
-
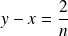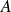et
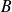sont des parties non vides de
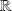car
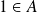et
. 
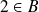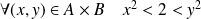. Donc :
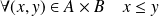.Soit
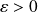. Montrons qu'il existe
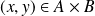tel que :
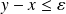.Si
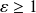, il existe
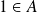et
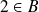tels que
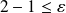.Si
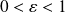, il existe un entier
non nul tel que :
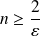.L'ensemble
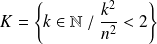est une partie de
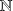non vide car
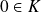, majorée p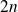ar
car
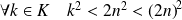. Donc
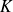a un plus grand élément
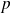. Donc :
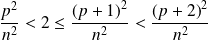. Donc
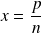appartient à
,
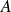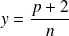appartient à
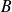et
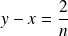, donc
.
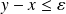Conclusion :
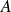et
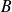sont deux parties adjacentes de
.
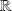Question
En déduire que
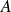n'a pas de borne supérieure dans
.
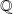Utilisez la première question et démontrez que la borne commune
vérifierait
.
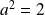D'après la première question :
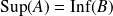. Soit
.
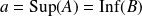Donc
majore
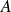et minore
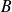. Or
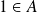et
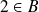. Donc
.
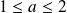Et :
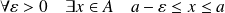. Donc
.
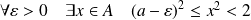Et :
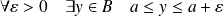. Donc
.
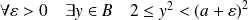Donc :
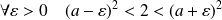, donc
.
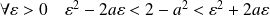En faisant tendre
vers
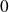, on obtient :
.
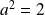Montrons que
n'est pas rationnel en raisonnant par l'absurde.
Supposons que
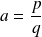avec
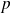et
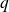entiers strictement positifs et premiers entre eux.
Donc :
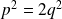. Or
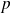et
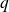sont premiers entre eux. Donc
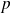divise
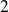. Donc
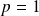ou
.
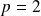Le cas
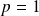ne convient pas car
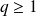, donc
.
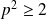Donc
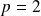, donc
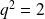, ce qui n'a pas de solution dans
.
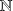Donc l'hypothèse était fausse. Donc
.
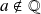Conclusion :
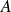n'a pas de borne supérieure dans
.
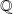