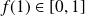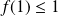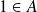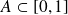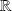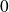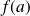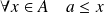Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
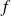une application croissante de
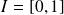dans lui-même, et
.
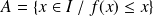Question
Question
Question
Démontrer que
.
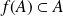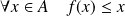, donc
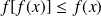car
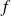est croissante, donc
.
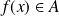Conclusion :
.
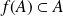Question
En déduire que
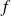possède un point fixe.
Montrez que
.
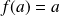est un minorant de
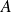, donc de
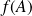. Donc :
.
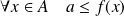En particulier
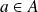, donc
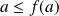. Mais
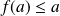car
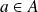. Donc :
.
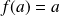Conclusion : L'application
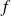possède un point fixe.
Remarque : Remarque
L'existence de
repose sur le fait que
.
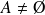Donc si
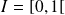, le raisonnement précédent ne serait plus possible. Cependant, on pourrait faire un raisonnement analogue avec la borne supérieure de
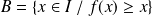car
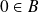. Donc dans ce cas aussi, l'application
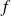possède un point fixe.
Par contre, si
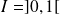, l'application
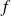n'a pas toujours un point fixe. Exemple :
.
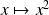