Cas de l'ensemble des réels
L'ensemble
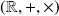 est un corps totalement ordonné.
est un corps totalement ordonné.
Définition :
L'ensemble des réels est archimédien :
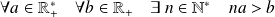 .
.
La partie entière d'un réel
 est le plus grand entier inférieur ou égal à
est le plus grand entier inférieur ou égal à
 :
:
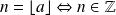 et
et
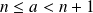 .
.
La partie fractionnaire d'un réel
 est :
est :
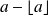 .
.
Fondamental :
Théorème des segments emboités :
Si
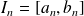 est une suite de segments emboités (
est une suite de segments emboités (
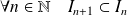 ) de
) de
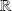 tels que
tels que
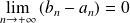 , alors
, alors
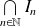 est réduite à un point.
est réduite à un point.
Conséquence : Si
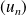 et
et
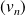 sont deux suites réelles adjacentes (monotones de sens contraires, dont la différence tend vers 0), alors elles sont convergentes et admettent la même limite.
sont deux suites réelles adjacentes (monotones de sens contraires, dont la différence tend vers 0), alors elles sont convergentes et admettent la même limite.
Fondamental :
Théorème de la borne supérieure (inférieure) :
Toute partie non vide majorée de
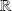 possède une borne supérieure :
possède une borne supérieure :
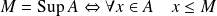 et
et
 .
.Toute partie non vide minorée de
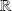 possède une borne inférieure :
possède une borne inférieure :
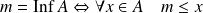 et
et
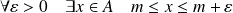 .
.
Conséquence :
Toute suite croissante majorée de réels est convergente.
Toute suite décroissante minorée de réels est convergente.





