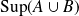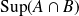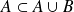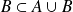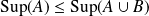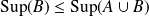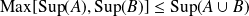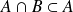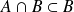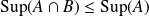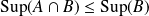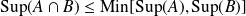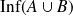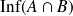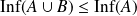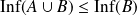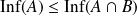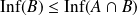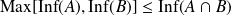Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
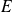un ensemble muni d'une relation d'ordre total notée
.
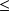Soit
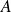et
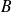deux parties de
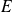qui admettent des bornes supérieures et des bornes inférieures.
Question
Si
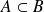, comparer
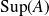et
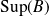, ainsi que
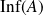et
.
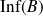Comparez les ensembles des majorants (puis des minorants) de
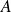et de
.
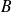Si
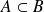, tout majorant de
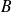est un majorant de
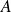. Donc
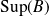est un majorant de
.
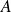Or
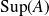est le plus petit majorant de
.
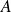Conclusion : Si
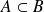, alors
.
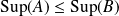Si
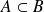, tout minorant de
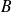est un minorant de
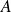. Donc
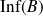est un minorant de
.
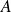Or
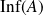est le plus grand des minorants de
.
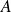Conclusion : Si
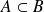, alors
.
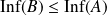Question
Question
Question
Soit
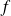une application croissante de
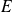dans
:
.
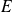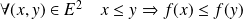Sous réserve d'existence, comparer
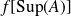et
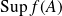, ainsi que
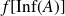et
.
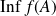Une borne supérieure (inférieure) est un majorant (minorant).
Déduisez des inégalités et utilisez le sens de variations de
.
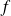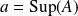est un majorant de
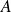et
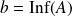est un minorant de
.
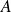Donc :
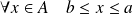. Or
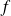est croissante. Donc :
.
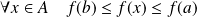Donc
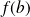est un minorant de
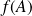. Donc :
.
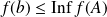Et
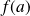est un majorant de
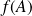. Donc :
.
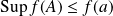Conclusion :
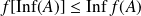et
.
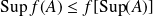