Exo 5
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
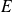 un ensemble muni d'une relation d'ordre total notée
un ensemble muni d'une relation d'ordre total notée
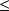 .
.
On définit sur
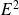 la relation :
la relation :
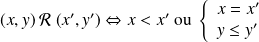 .
.
Question
Démontrer que la relation
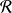 est une relation d'ordre total sur
est une relation d'ordre total sur
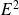 . On appelle cette relation l'ordre lexicographique.
. On appelle cette relation l'ordre lexicographique.
Pour démontrer l'antisymétrie et la transitivité, étudiez les quatre cas possibles.
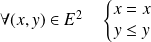 , donc
, donc
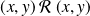 .
.Donc la relation
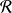 est réflexive
est réflexive
Montrons qu'elle est antisymétrique. Supposons que
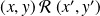 et que
et que
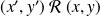 .
.On a donc :
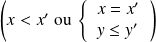 et
et
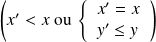 .
.Il y a donc quatre cas :
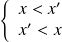 ou
ou
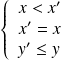 ou
ou
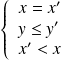 ou
ou
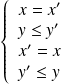 .
.Les trois premiers systèmes n'ont pas de solution. Et le quatrième système équivaut à
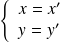 , donc à
, donc à
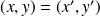 .
.Donc la relation
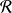 est antisymétrique.
est antisymétrique.
Montrons que la relation
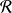 est transitive. Supposons que
est transitive. Supposons que
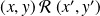 et que
et que
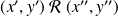 .
.On a donc :
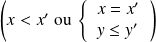 et
et
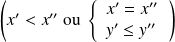 .
.Il y a donc quatre cas :
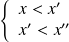 ou
ou
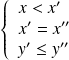 ou
ou
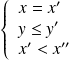 ou
ou
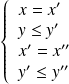 .
.Donc :
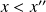 ou
ou
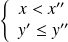 ou
ou
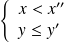 ou
ou
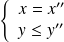 . Donc
. Donc
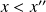 ou
ou
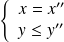 .
.Donc
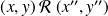 .
.Donc la relation
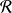 est transitive.
est transitive.
Donc la relation
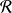 est une relation d'ordre.
est une relation d'ordre.
Soient
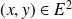 et
et
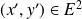 .
.
Si
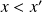 , alors
, alors
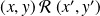 . Si
. Si
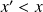 , alors
, alors
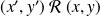 .
.
Si
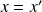 , alors
, alors
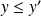 ou
ou
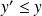 , donc
, donc
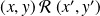 ou
ou
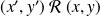 .
.
Conclusion : La relation
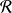 est une relation d'ordre total.
est une relation d'ordre total.
Remarque : Remarque
On peut généraliser par récurrence pour définir une relation d'ordre total sur
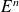 .
.
C'est par exemple l'ordre utilisé dans un dictionnaire, qui est défini à partir de l'ordre des lettres dans l'alphabet.
Question
En déduire que l'on peut définir sur
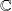 une relation d'ordre total qui prolonge la relation d'ordre sur
une relation d'ordre total qui prolonge la relation d'ordre sur
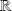 , mais que
, mais que
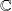 n'est pas un corps ordonné pour cette relation d'ordre.
n'est pas un corps ordonné pour cette relation d'ordre.
Définissez la relation d'ordre en utilisant les parties réelles et imaginaires des complexes.
Montrez que si la relation était compatible avec la multiplication, on aurait :
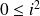 .
.
Tout complexe a une unique forme algébrique :
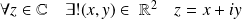 .
.
On définit sur
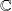 la relation :
la relation :
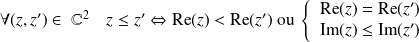 .
.
C'est une relation d'ordre total sur
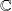 car elle correspond à l'ordre lexicographique sur
car elle correspond à l'ordre lexicographique sur
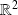 .
.
On peut remarquer que si
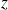 et
et
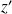 sont réels, alors
sont réels, alors
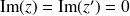 , donc
, donc
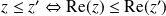 . Donc on retrouve la relation d'ordre sur
. Donc on retrouve la relation d'ordre sur
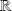 .
.
Conclusion : On peut définir une relation d'ordre total sur
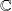 qui prolonge la relation d'ordre sur
qui prolonge la relation d'ordre sur
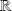 .
.
Avec cette relation d'ordre, on a :
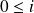 car
car
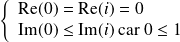 .
.
Donc si
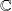 était un corps ordonné, on aurait
était un corps ordonné, on aurait
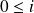 et
et
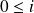 , donc
, donc
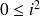 , donc
, donc
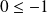 , ce qui est évidemment faux.
, ce qui est évidemment faux.
Conclusion : Cette relation d'ordre ne munit pas
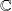 d'une structure de corps ordonné.
d'une structure de corps ordonné.
Question
Pour cette relation d'ordre, l'ensemble
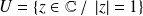 est-il majoré ? A-t-il une borne supérieure ?
est-il majoré ? A-t-il une borne supérieure ?
Comparez les éléments de
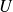 avec
avec
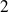 .
.
Plus généralement, déterminez l'ensemble des majorants de
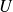 .
.
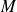 est un majorant de
est un majorant de
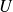 si et seulement si :
si et seulement si :
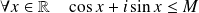 , donc si :
, donc si :
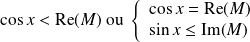 .
.
Donc
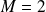 majore
majore
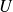 .
.
Conclusion : L'ensemble
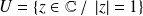 est majoré.
est majoré.
L'ensemble
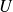 admet une borne supérieure si et seulement si l'ensemble
admet une borne supérieure si et seulement si l'ensemble
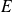 des majorants de
des majorants de
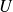 a un plus petit élément.
a un plus petit élément.
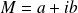 appartient à
appartient à
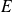 si et seulement si
si et seulement si
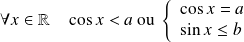 .
.
En particulier, pour
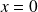 , il faut que :
, il faut que :
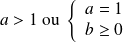 .
.
Réciproquement si
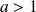 , alors
, alors
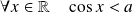 , donc
, donc
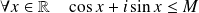 .
.
Si
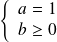 , alors
, alors
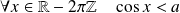 et
et
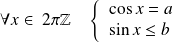 car
car
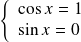 .
.
Donc, si
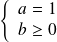 , alors
, alors
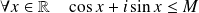 .
.
Donc
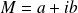 appartient à
appartient à
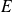 si et seulement si
si et seulement si
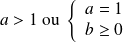 .
.
L'ensemble des majorants de
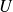 est :
est :
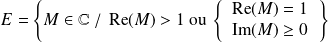 .
.
Or dans
 :
:
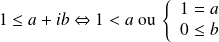 si
si
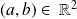 .
.
Donc
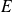 est l'ensemble des complexes
est l'ensemble des complexes
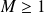 . Donc
. Donc
 est le plus petit majorant de
est le plus petit majorant de
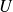 .
.
Conclusion : L'ensemble
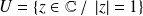 admet
admet
 comme borne supérieure.
comme borne supérieure.





