Relation d'ordre
Rappel :
Une relation d'ordre sur un ensemble
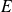 est une relation binaire réflexive, antisymétrique et transitive.
est une relation binaire réflexive, antisymétrique et transitive.
L'ordre est total si :
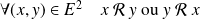 . Sinon l'ordre est partiel.
. Sinon l'ordre est partiel.
Exemple :
L'ensemble
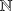 des entiers naturels est muni d'une relation d'ordre total compatible avec l'addition et la multiplication.
des entiers naturels est muni d'une relation d'ordre total compatible avec l'addition et la multiplication.L'ensemble
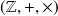 des entiers relatifs est un anneau totalement ordonné.
des entiers relatifs est un anneau totalement ordonné.L'ensemble
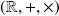 est un corps totalement ordonné.
est un corps totalement ordonné.
Sur
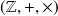 et
et
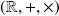 , la relation d'ordre est compatible avec l'addition, mais pas avec la multiplication.
, la relation d'ordre est compatible avec l'addition, mais pas avec la multiplication.
On a un anneau ou un corps ordonné si, pour tous
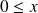 et
et
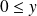 , on a
, on a
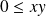 .
.
Par contre, le corps des complexes
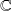 n'est pas un corps ordonné.
n'est pas un corps ordonné.
Définition :
Si
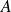 est une partie non vide de
est une partie non vide de
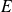 et si la relation d'ordre est totale et notée
et si la relation d'ordre est totale et notée
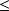 :
:
 est un majorant de
est un majorant de
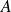 si :
si :
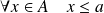 .
. est un minorant de
est un minorant de
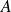 si :
si :
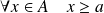 .
. est un plus grand élément de
est un plus grand élément de
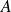 si :
si :
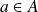 et
et
 est un majorant.
est un majorant. est un plus petit élément de
est un plus petit élément de
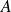 si :
si :
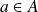 et
et
 est un minorant.
est un minorant. est borne supérieure de
est borne supérieure de
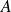 si
si
 est le plus petit des majorants.
est le plus petit des majorants. est borne inférieure de
est borne inférieure de
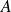 si
si
 est le plus grand des minorants.
est le plus grand des minorants.
Ces éléments n'existent pas toujours.
Exemple :
Toute partie non vide de
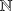 possède un plus petit élément.
possède un plus petit élément.
Toute partie non vide majorée de
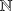 possède un plus grand élément, mais l'ensemble
possède un plus grand élément, mais l'ensemble
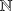 n'a pas de plus grand élément.
n'a pas de plus grand élément.
Fondamental :
Principe de récurrence :
Si une propriété
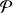 définie sur
définie sur
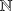 vérifie les deux axiomes suivants :
vérifie les deux axiomes suivants :
Initialisation :
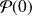 est vraie.
est vraie.Hérédité : Pour tout entier
 tel que
tel que
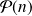 est vraie, alors
est vraie, alors
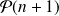 est vraie.
est vraie.
Alors la propriété
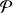 est vraie pour tout entier
est vraie pour tout entier
 de
de
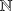 .
.





