Exo 4
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
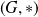et
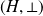deux groupes d'éléments neutres respectifs
et
.
Soit
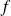un morphisme de
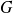dans
.
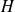Question
Montrer que si
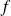est un morphisme de
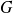dans
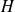, son noyau
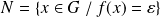est un sous groupe distingué de
.
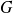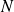est une partie non vide de
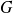car
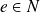. En effet,
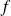est un morphisme donc
.
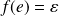Soient
et
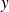deux éléments de
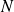. Donc
.
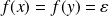L'image du symétrique
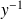de
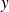dans
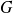est le symétrique
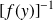de
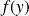dans
.
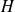Donc :
.
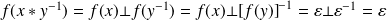Donc :
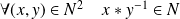. Donc
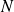est un sous-groupe de
.
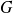Soient
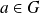et
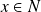, donc
.
.
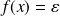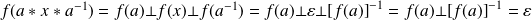Donc :
.
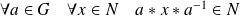Conclusion :
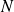est un sous-groupe distingué de
.
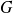Question
Démontrer que le groupe quotient
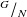est isomorphe à
.
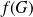Démontrez que deux éléments
et
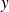appartiennent à la même classe d'équivalence si et seulement si :
.
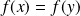L'ensemble quotient
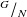est l'ensemble des classes d'équivalence pour la relation :
.
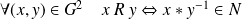Donc
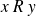si et seulement si
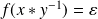, donc si
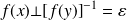, donc si
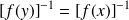, donc si
.
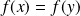La classe d'équivalence de
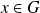est :
.
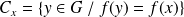Soit
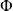l'application qui, à tout
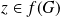, associe
.
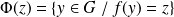Or, pout tout
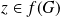, il existe au moins un
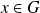tel que
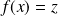. On a alors :
.
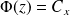Donc
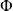est une application de
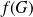dans
.
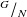Tout élément
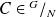est une classe d'équivalence. Donc, il existe
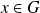tel que
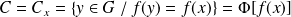. Donc l'application
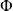est surjective.
Et
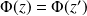si et seulement si
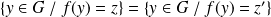, donc si
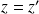. Donc l'application
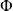est injective.
Donc
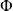est une bijection de
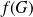dans
.
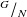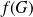muni de la loi
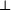est un sous-groupe de
.
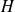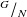a une structure de groupe lorsqu'il est muni de la loi :
.
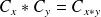Soit
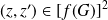. Il existe
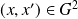tel que
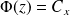et
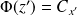, donc
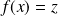et
.
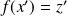Donc
.
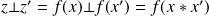Donc :
.
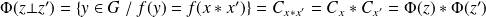Donc
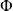est un isomorphisme de
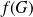dans
.
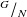Conclusion : Le groupe quotient
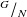est isomorphe à
.
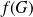Question
En déduire que
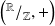est isomorphe à
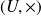où
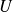est l'ensemble des nombres complexes de module
.
Utilisez les résultats précédents pour l'application
:
.
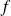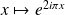L'application
:
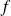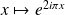est un morphisme de
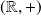dans
.
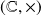Donc :
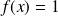si et seulement si
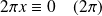, donc si
.
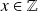Donc son noyau est :
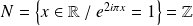. Et son image est :
.
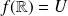On applique le résultat précédent.
Conclusion :
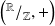est isomorphe à
.
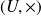