Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
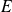 un ensemble et
un ensemble et
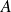 une partie non vide de
une partie non vide de
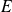 .
.
On définit sur
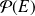 la relation binaire :
la relation binaire :
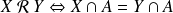 .
.
Question
Démontrer que la relation
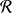 est une relation d'équivalence.
est une relation d'équivalence.
Les propriétés de la relation
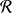 sont conséquences directes de celles de l'égalité :
sont conséquences directes de celles de l'égalité :
Elle est réflexive puisque :
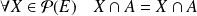 , donc
, donc
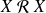 .
.
Elle est symétrique puisque :
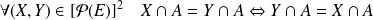 , donc
, donc
 .
.
Elle est transitive puisque :
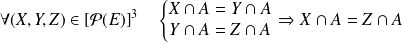 , donc
, donc
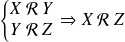 .
.
Conclusion : La relation
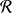 est une relation d'équivalence.
est une relation d'équivalence.
Question
Démontrer qu'il existe une bijection
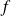 entre l'ensemble quotient
entre l'ensemble quotient
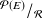 et
et
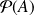 .
.
A toute partie de
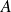 , faites correspondre sa classe d'équivalence.
, faites correspondre sa classe d'équivalence.
Démontrez que l'application est bijective.
L'ensemble quotient
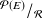 est l'ensemble des classes d'équivalence.
est l'ensemble des classes d'équivalence.
Soit
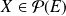 . Notons
. Notons
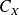 la classe d'équivalence de
la classe d'équivalence de
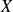 .
.
Une partie
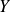 de
de
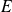 appartient à
appartient à
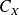 si et seulement si
si et seulement si
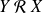 , donc si
, donc si
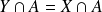 . Or :
. Or :
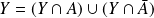 . Donc si
. Donc si
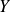 appartient à la classe d'équivalence de
appartient à la classe d'équivalence de
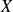 , alors il existe
, alors il existe
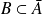 tel que :
tel que :
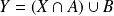 .
.
Réciproquement, si
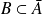 et
et
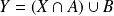 , alors
, alors
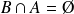 , donc
, donc
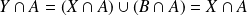 , donc
, donc
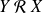 , donc
, donc
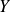 appartient à
appartient à
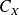 .
.
Donc :
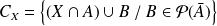 .
.
Soit
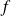 l'application de
l'application de
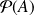 dans
dans
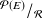 qui à toute partie
qui à toute partie
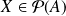 associe sa classe d'équivalence :
associe sa classe d'équivalence :
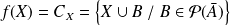 .
.
Donc :
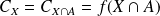 pour toute partie
pour toute partie
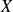 de
de
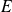 . Donc
. Donc
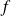 est surjective.
est surjective.
Et pour toutes parties
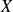 et
et
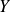 de
de
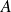 ,
,
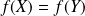 si et seulement si
si et seulement si
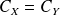 , donc si
, donc si
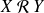 , donc si
, donc si
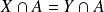 , donc si
, donc si
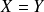 . Donc
. Donc
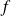 est injective.
est injective.
Donc l'application
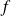 est bijective.
est bijective.
Conclusion : Il existe une bijection
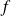 entre l'ensemble quotient
entre l'ensemble quotient
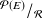 et
et
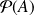 .
.
Question
Montrer que la relation
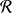 est compatible avec la loi
est compatible avec la loi
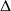 (différence symétrique).
(différence symétrique).
Si
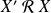 , il existe
, il existe
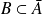 tel que
tel que
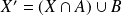 .
.
Démontrez que, si
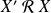 , alors pour tout
, alors pour tout
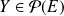 :
:
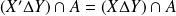 .
.
Supposons que
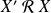 et
et
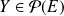 .
.
Donc il existe
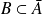 tel que
tel que
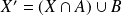 . Donc :
. Donc :
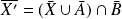 .
.
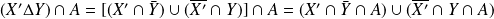 .
.
Donc :
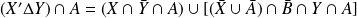 . Or
. Or
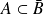 .
.
Donc :
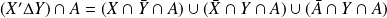 . Or
. Or
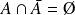 .
.
Donc :
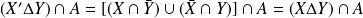 .
.
Donc si
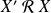 , alors pour tout
, alors pour tout
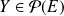 , on a :
, on a :
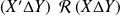 .
.
Or la loi
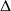 est commutative.
est commutative.
Donc si
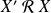 et
et
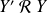 , on a
, on a
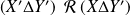 et
et
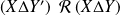 .
.
Donc par transitivité, si
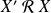 et
et
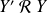 , alors
, alors
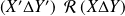 .
.
Conclusion : La relation
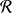 est compatible avec la loi
est compatible avec la loi
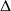 .
.
Question
En déduire que
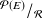 peut être muni d'une structure de groupe. L'application
peut être muni d'une structure de groupe. L'application
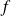 est-elle un isomorphisme de groupes ?
est-elle un isomorphisme de groupes ?
C'est le cours !
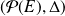 est un groupe commutatif.
est un groupe commutatif.
Conclusion :
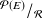 peut être muni d'une structure de groupe commutatif.
peut être muni d'une structure de groupe commutatif.
La loi sur
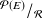 est définie par :
est définie par :
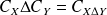 .
.
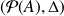 est un groupe commutatif.
est un groupe commutatif.
Et pour tous
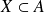 et
et
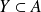 :
:
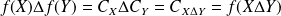 .
.
Conclusion : L'application
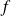 est un isomorphisme de groupes de
est un isomorphisme de groupes de
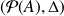 dans
dans
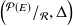 .
.
Question
Montrer que
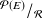 peut aussi être muni d'une structure d'anneau. L'application
peut aussi être muni d'une structure d'anneau. L'application
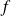 est-elle un isomorphisme d'anneaux ?
est-elle un isomorphisme d'anneaux ?
Démontrez que la relation
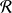 est aussi compatible avec la loi
est aussi compatible avec la loi
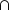 , puis que l'application
, puis que l'application
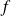 est un isomorphisme d'anneaux.
est un isomorphisme d'anneaux.
Si
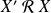 et
et
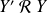 , alors :
, alors :
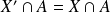 et
et
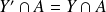 .
.
Donc :
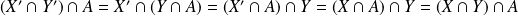 .
.
Donc la relation
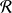 est compatible avec la loi
est compatible avec la loi
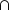 .
.
Or
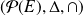 est un anneau commutatif.
est un anneau commutatif.
Conclusion :
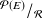 peut être muni d'une structure d'anneau commutatif.
peut être muni d'une structure d'anneau commutatif.
Les lois sur
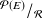 sont définies par :
sont définies par :
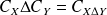 et
et
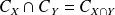 .
.
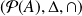 est un anneau commutatif.
est un anneau commutatif.
Et pour tous
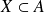 et
et
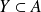 :
:
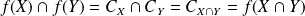 .
.
Conclusion : L'application
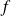 est un isomorphisme d'anneaux de
est un isomorphisme d'anneaux de
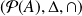 dans
dans
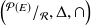 .
.





