Relation d'équivalence
Rappel :
Une relation d'équivalence sur un ensemble
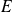 est une relation binaire réflexive, symétrique et transitive.
est une relation binaire réflexive, symétrique et transitive.
Définition :
Si
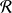 est une relation d'équivalence sur
est une relation d'équivalence sur
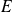 , la classe d'équivalence d'un élément
, la classe d'équivalence d'un élément
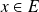 est :
est :
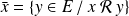 .
.
Donc
 .
.
Les classes d'équivalence forment une partition de
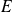 .
.
L'ensemble quotient
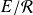 est l'ensemble de toutes les classes d'équivalence.
est l'ensemble de toutes les classes d'équivalence.
Si
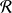 est compatible avec une loi de composition interne
est compatible avec une loi de composition interne
 sur
sur
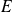 , l'ensemble quotient
, l'ensemble quotient
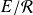 peut être muni de la loi de composition interne (notée aussi
peut être muni de la loi de composition interne (notée aussi
 ) :
) :
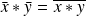 .
.
Exemple :
Sur l'ensemble des couples de points du plan, la relation "
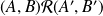 si les segments
si les segments
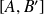 et
et
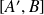 ont même milieu" est une relation d'équivalence.
ont même milieu" est une relation d'équivalence.
La classe d'équivalence de
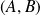 est le vecteur
est le vecteur
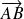 . L'ensemble quotient est l'ensemble des vecteurs du plan.
. L'ensemble quotient est l'ensemble des vecteurs du plan.
Fondamental :
Relations d'équivalence dans un groupe :
Si
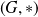 est un groupe et
est un groupe et
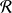 une relation d'équivalence compatible avec la loi
une relation d'équivalence compatible avec la loi
 , alors
, alors
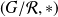 est un groupe.
est un groupe.Si
 est l'élément neutre de
est l'élément neutre de
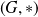 :
:
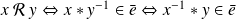
Si
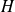 est un sous-groupe de
est un sous-groupe de
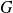 , on lui associe deux relations d'équivalence :
, on lui associe deux relations d'équivalence :la relation d'équivalence modulo
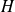 à gauche :
à gauche :
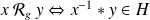 .
.
la relation d'équivalence modulo
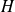 à droite :
à droite :
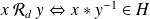 .
.
Elles sont compatibles avec la loi
 si et seulement si
si et seulement si
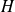 est un sous-groupe distingué de
est un sous-groupe distingué de
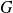 :
:
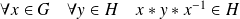 .
.Si
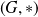 est un groupe fini, les nombres de classes d'équivalence modulo
est un groupe fini, les nombres de classes d'équivalence modulo
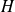 à gauche et à droite sont égaux. C'est l'indice
à gauche et à droite sont égaux. C'est l'indice
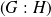 de
de
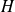 dans
dans
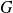 et
et
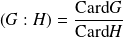 .
.
Fondamental :
Relations d'équivalence dans un anneau :
Si
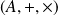 est un anneau et
est un anneau et
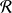 une relation d'équivalence compatible avec les deux lois, alors
une relation d'équivalence compatible avec les deux lois, alors
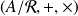 est un anneau.
est un anneau.Si
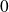 est l'élément neutre de l'addition :
est l'élément neutre de l'addition :
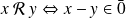 .
.
Si
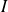 est un idéal de
est un idéal de
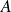 , on lui associe la relation d'équivalence modulo
, on lui associe la relation d'équivalence modulo
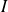 :
:
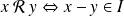 .
.Cette relation est compatible avec les deux lois, et l'anneau quotient est noté
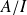 .
.Si l'anneau
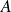 est commutatif :
est commutatif :l'anneau
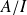 est un corps si et seulement si l'idéal
est un corps si et seulement si l'idéal
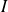 est maximal (il n'existe pas d'idéal plus grand sauf
est maximal (il n'existe pas d'idéal plus grand sauf
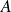 ).
).l'anneau
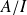 est un anneau intègre si et seulement si l'idéal
est un anneau intègre si et seulement si l'idéal
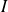 est premier :
est premier :
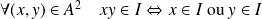 .
.





