Exo 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
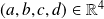 avec
avec
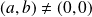 et
et
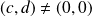 .
.
Soit
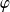 l'application définie par :
l'application définie par :
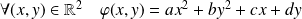 .
.
On définit une relation binaire
 sur
sur
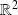 par :
par :
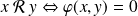 .
.
Question
A quelle condition la relation
 est-elle réflexive ?
est-elle réflexive ?
Remarque :
On peut remarquer que la représentation du graphe
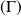 de cette relation est une conique passant par l'origine du repère.
de cette relation est une conique passant par l'origine du repère.
La relation
 est réflexive si et seulement si :
est réflexive si et seulement si :
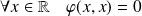 , donc si et seulement si :
, donc si et seulement si :
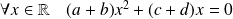 .
.
Un polynôme est nul si et seulement si tous ses coefficients sont nuls.
Donc la relation
 est réflexive si et seulement si :
est réflexive si et seulement si :
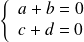 .
.
Conclusion : La relation
 est réflexive si et seulement si :
est réflexive si et seulement si :
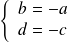 .
.
Alors :
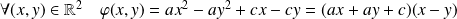 avec
avec
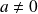 et
et
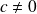 .
.
Donc la conique
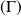 est la réunion des droites d'équations
est la réunion des droites d'équations
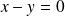 et
et
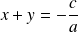 .
.
Question
A quelle condition la relation
 est-elle symétrique ?
est-elle symétrique ?
La relation est symétrique si et seulement si
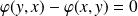 pour tout
pour tout
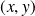 du graphe.
du graphe.
La relation
 est symétrique si et seulement si :
est symétrique si et seulement si :
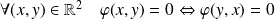 .
.
Donc la relation
 est symétrique si et seulement si :
est symétrique si et seulement si :
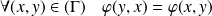 .
.
Or :
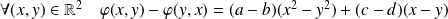 .
.
Donc :
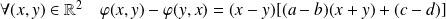 .
.
Donc la relation
 est symétrique si et seulement si :
est symétrique si et seulement si :
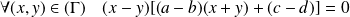 .
.
Donc
 est symétrique si et seulement si :
est symétrique si et seulement si :
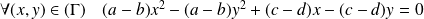 , propriété notée
, propriété notée
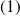 .
.
Si
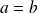 et
et
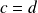 , la propriété
, la propriété
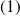 est vérifiée pour tout
est vérifiée pour tout
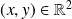 , donc pour tout
, donc pour tout
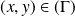 .
. Donc
 est symétrique.
est symétrique.
Si
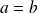 et
et
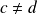 , la propriété
, la propriété
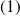 est vérifiée si
est vérifiée si
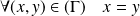 .
. Alors :
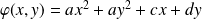 avec
avec
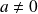 , et
, et
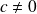 ou
ou
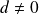 . Donc
. Donc
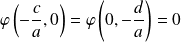 .
. Or
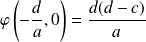 et
et
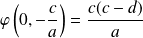 . L'un au moins des deux est non nul.
. L'un au moins des deux est non nul. Donc
 n'est donc pas symétrique.
n'est donc pas symétrique.Si
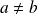 , la propriété
, la propriété
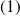 est vérifiée si et seulement si :
est vérifiée si et seulement si :
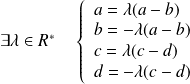 , donc si
, donc si
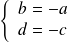 .
.
Conclusion : La relation
 est symétrique si et seulement si
est symétrique si et seulement si
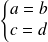 ou si
ou si
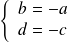 .
.
Dans le premier cas :
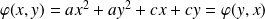 .
.
La conique
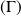 est le cercle de centre
est le cercle de centre
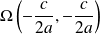 et de rayon
et de rayon
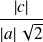 .
.
Dans le deuxième cas :
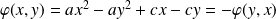 .
.
La conique
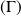 est la réunion de deux droites d'équations
est la réunion de deux droites d'équations
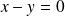 et
et
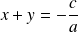 .
.
Dans les deux cas, la conique est symétrique par rapport à la droite d'équation
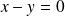 .
.
Question
La relation
 peut-elle être une relation d'équivalence ?
peut-elle être une relation d'équivalence ?
Démontrez que, si elle est réflexive, on peut factoriser
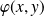 .
.
Démontrer qu'elle est alors symétrique et transitive.
Pour que la relation
 soit une relation d'équivalence, il faut qu'elle soit réflexive et symétrique, donc il faut que
soit une relation d'équivalence, il faut qu'elle soit réflexive et symétrique, donc il faut que
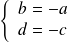 .
.
Donc :
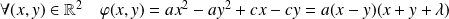 en posant
en posant
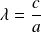 .
.
Il faut de plus qu'elle soit transitive, donc que :
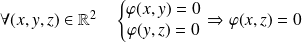 .
.
Or :
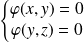 équivaut à
équivaut à
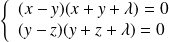 .
.
Donc, si
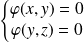 , il y a quatre cas :
, il y a quatre cas :
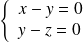 ce qui implique
ce qui implique
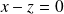 , donc
, donc
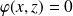 .
.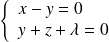 ce qui implique
ce qui implique
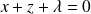 , donc
, donc
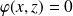 .
.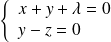 ce qui implique
ce qui implique
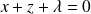 , donc
, donc
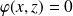 .
.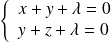 ce qui implique
ce qui implique
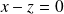 , donc
, donc
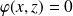 .
.
Donc si
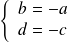 , la relation
, la relation
 est transitive.
est transitive.
Conclusion : La relation
 est une relation d'équivalence si et seulement si
est une relation d'équivalence si et seulement si
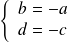 .
.
Question
La relation
 peut-elle être une relation d'ordre ?
peut-elle être une relation d'ordre ?
Démontrez que, si elle est réflexive, alors elle n'est pas antisymétrique (trouvez un contre-exemple).
Pour que la relation
 soit une relation d'ordre, il faut qu'elle soit réflexive, donc il faut que
soit une relation d'ordre, il faut qu'elle soit réflexive, donc il faut que
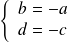 .
.
D'après les calculs précédents, la relation
 est alors transitive.
est alors transitive.
On a :
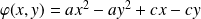 . Donc
. Donc
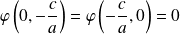 et
et
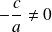 .
.
Donc
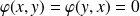 n'implique pas
n'implique pas
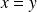 .
.
Donc la relation
 n'est pas antisymétrique.
n'est pas antisymétrique.
Conclusion : La relation
 ne peut pas être une relation d'ordre.
ne peut pas être une relation d'ordre.
Complément :
La recherche d'une condition pour que
 soit antisymétrique est beaucoup plus compliquée.
soit antisymétrique est beaucoup plus compliquée.
La relation
 est antisymétrique si et seulement si :
est antisymétrique si et seulement si :
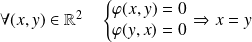 .
.
Donc la relation
 est antisymétrique si et seulement si :
est antisymétrique si et seulement si :
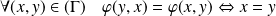 .
.
Or :
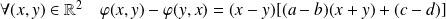 .
.
Donc :
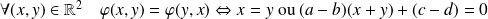 .
.
Si
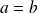 et
et
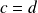 , alors
, alors
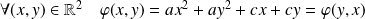 .
.Donc :
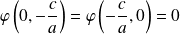 et
et
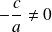 . Donc
. Donc
 n'est pas antisymétrique.
n'est pas antisymétrique.Si
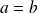 et
et
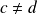 , alors
, alors
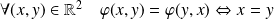 . C'est vrai en particulier pour tout
. C'est vrai en particulier pour tout
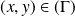 .
. Donc
 est antisymétrique.
est antisymétrique.Si
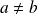 , alors
, alors
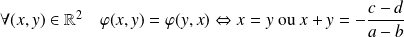 .
.Donc
 est antisymétrique si
est antisymétrique si
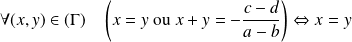 , donc si dans
, donc si dans
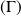 il n'existe pas de couple
il n'existe pas de couple
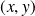 tel que
tel que
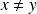 et
et
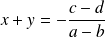 .
.Or si
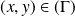 et
et
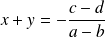 , alors :
, alors :
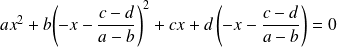 .
.Donc :
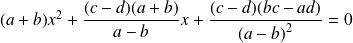 équation notée
équation notée
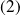 .
.Si
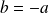 , on obtient
, on obtient
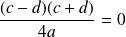 .
.Si
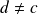 et
et
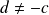 , il n'existe pas de couple
, il n'existe pas de couple
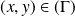 tel que
tel que
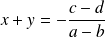 .
.Donc
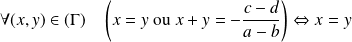 .
.Donc
 est antisymétrique.
est antisymétrique.Si
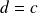 :
:
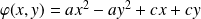 . Donc
. Donc
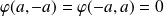 et
et
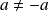 .
.Donc
 n'est pas antisymétrique.
n'est pas antisymétrique.Si
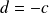 :
:
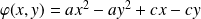 . Donc :
. Donc :
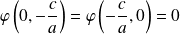 et
et
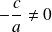 .
.Donc
 n'est pas antisymétrique.
n'est pas antisymétrique.
Si
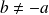 , l'équation
, l'équation
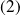 est une équation du second degré.
est une équation du second degré.Son discriminant est :
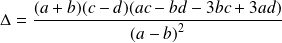 .
.Si
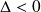 , il n'existe pas de couple
, il n'existe pas de couple
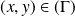 tel que
tel que
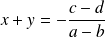 .
.Donc
 est antisymétrique.
est antisymétrique.Si
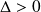 , il existe deux couples distincts
, il existe deux couples distincts
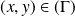 tel que
tel que
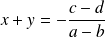 .
.Pour que
 soit antisymétrique, il faut que ces couples vérifient
soit antisymétrique, il faut que ces couples vérifient
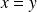 .
. Or la seule possibilité est
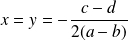 . Donc au plus un couple convient.
. Donc au plus un couple convient.Donc
 n'est pas antisymétrique.
n'est pas antisymétrique.Si
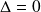 , l'équation
, l'équation
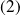 a une racine double
a une racine double
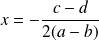 , donc
, donc
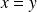 .
.Donc
 est antisymétrique.
est antisymétrique.
Conclusion : La relation
 est antisymétrique si
est antisymétrique si
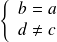 ou
ou
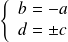 ou
ou
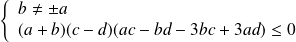 .
.





