Relation binaire
Définition :
Une relation binaire dans un ensemble
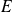est déterminée par une partie
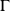non vide de
:
.
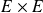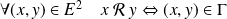La partie
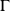de
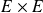est le graphe de la relation binaire associée.
Fondamental :
Propriétés :
La relation est réflexive si :
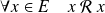.La relation est symétrique si :
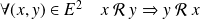.La relation est antisymétrique si :
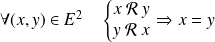.La relation est transitive si :
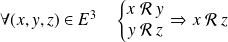.La relation est compatible avec la loi de composition interne
sur
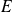si :
.
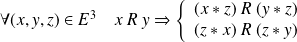Définition :
Une relation d'équivalence sur un ensemble
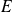est une relation binaire réflexive, symétrique et transitive.
Exemple :
L'égalité est une relation d'équivalence sur tout ensemble
.
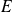Définition :
Une relation d'ordre sur un ensemble
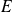est une relation binaire réflexive, antisymétrique et transitive.
L'ordre est total si :
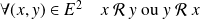. Sinon l'ordre est partiel.
Exemple :
L'inclusion est une relation d'ordre partiel sur l'ensemble des parties d'un ensemble
.
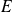