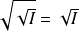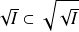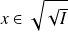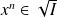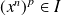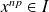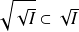Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
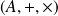 un anneau commutatif.
un anneau commutatif.
Pour tout idéal
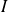 de
de
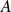 , on définit :
, on définit :
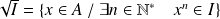 .
.
Question
Déterminer
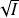 si
si
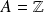 et si
et si
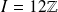 .
.
Utilisez les divisibilités.
Soit
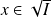 . Donc il existe un entier
. Donc il existe un entier
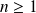 tel que
tel que
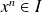 , donc tel que
, donc tel que
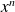 soit divisible par
soit divisible par
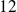 .
.
Donc
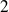 et
et
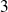 divisent
divisent
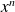 , donc ils divisent
, donc ils divisent
 puisqu'ils sont premiers.
puisqu'ils sont premiers.
Donc
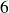 divise
divise
 puisque
puisque
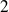 et
et
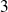 sont premiers entre eux. Donc
sont premiers entre eux. Donc
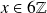 .
.
Donc :
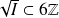 .
.
Réciproquement si
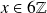 ,
,
 est divisible par
est divisible par
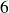 , donc
, donc
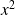 est divisible par
est divisible par
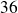 , donc par
, donc par
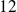 . Donc
. Donc
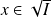 .
.
Donc :
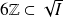 .
.
Conclusion :
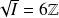 .
.
Question
Soit
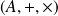 un anneau commutatif.
un anneau commutatif.
Démontrer que
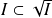 pour tout idéal
pour tout idéal
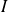 de
de
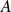 , et que si
, et que si
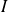 et
et
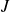 sont deux idéaux tels que
sont deux idéaux tels que
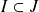 , alors
, alors
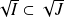 .
.
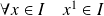 , donc
, donc
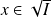 .
.
Conclusion :
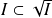 .
.
Si
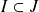 , pour tout
, pour tout
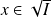 , il existe un entier
, il existe un entier
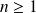 tel que
tel que
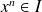 , donc
, donc
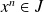 , donc
, donc
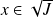 .
.
Conclusion : Si
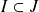 , alors
, alors
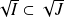 .
.
Question
Démontrer que
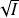 est un idéal de
est un idéal de
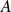 .
.
Pour démontrer que
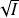 est un sous-groupe additif de
est un sous-groupe additif de
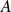 , utilisez la formule du binôme de Newton.
, utilisez la formule du binôme de Newton.
Soit
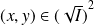 . Donc il existe des entiers
. Donc il existe des entiers
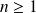 et
et
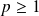 tels que
tels que
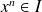 et
et
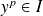 .
.L'anneau est commutatif, donc :
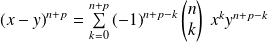 .
.Si
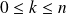 , alors
, alors
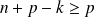 , donc
, donc
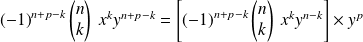 est le produit d'un élément de
est le produit d'un élément de
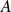 par un élément de
par un élément de
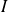 , donc appartient à
, donc appartient à
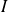 .
.Si
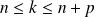 , alors
, alors
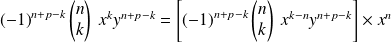 est le produit d'un élément de
est le produit d'un élément de
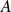 par un élément de
par un élément de
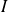 , donc appartient à
, donc appartient à
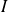 .
.Or
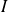 est un idéal, donc stable par addition. Donc
est un idéal, donc stable par addition. Donc
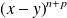 appartient à
appartient à
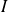 . Donc
. Donc
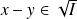 .
.
Soit
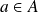 et
et
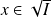 . Donc il existe un entier
. Donc il existe un entier
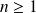 tel que
tel que
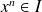 .
.Or
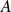 est un anneau. Donc
est un anneau. Donc
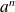 appartient à
appartient à
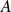 . Et
. Et
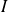 est un idéal de
est un idéal de
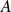 , donc
, donc
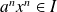 .
. Or l'anneau est commutatif, donc :
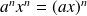 . Donc
. Donc
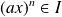 . Donc
. Donc
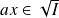 .
.
Conclusion :
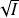 est un idéal de
est un idéal de
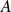 .
.
Question
Question
Si
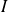 et
et
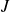 sont deux idéaux de
sont deux idéaux de
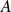 , démontrer que :
, démontrer que :
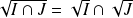 .
.
Démontrez successivement les deux inclusions.
Montrons successivement les deux inclusions.
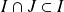 et
et
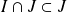 . Donc d'après la deuxième question :
. Donc d'après la deuxième question :
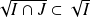 et
et
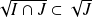 .
. Donc :
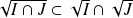 .
.
Inversement, soit
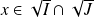 , donc
, donc
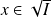 et
et
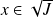 .
.Donc il existe deux entiers
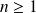 et
et
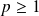 tels que
tels que
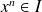 et
et
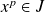 .
.Donc
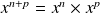 est produit d'un élément de
est produit d'un élément de
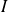 par un élément de
par un élément de
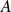 , donc
, donc
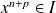 .
.De même
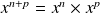 est produit d'un élément de
est produit d'un élément de
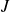 par un élément de
par un élément de
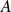 , donc
, donc
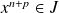 .
.Donc
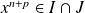 . Donc
. Donc
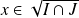 . Donc :
. Donc :
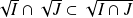 .
.
Conclusion :
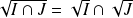 .
.
Question
Si
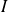 et
et
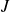 sont deux idéaux de
sont deux idéaux de
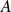 , démontrer que :
, démontrer que :
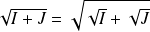 .
.
Démontrez successivement les deux inclusions.
Utilisez la formule du binôme de Newton.
Montrons que
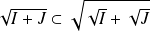 .
.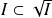 et
et
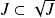 . Donc :
. Donc :
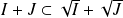 .
. Donc :
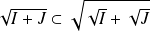 .
.Montrons que
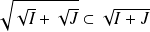 .
. Soit
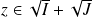 . Donc
. Donc
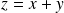 avec
avec
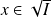 et
et
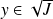 .
.Donc il existe des entiers
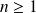 et
et
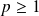 tels que
tels que
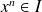 et
et
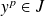 .
.L'anneau est commutatif, donc :
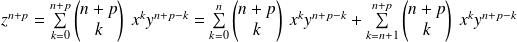 .
.Si
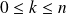 , alors
, alors
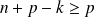 , donc
, donc
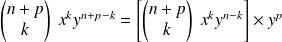 est le produit d'un élément de
est le produit d'un élément de
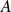 par un élément de
par un élément de
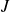 , donc appartient à
, donc appartient à
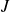 . Donc
. Donc
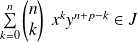 .
.Si
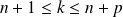 , alors
, alors
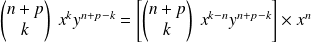 est le produit d'un élément de
est le produit d'un élément de
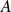 par un élément de
par un élément de
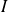 , donc appartient à
, donc appartient à
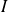 . Donc
. Donc
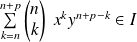 .
.Donc
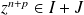 . Donc
. Donc
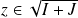 .
.Donc :
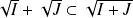 . Donc :
. Donc :
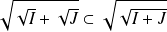 . Or :
. Or :
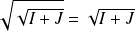 .
.Donc :
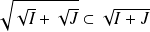 .
.
Conclusion :
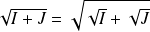 .
.