Exo 5
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
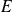 un ensemble non vide et
un ensemble non vide et
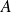 l'ensemble des applications de
l'ensemble des applications de
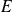 dans
dans
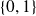 .
.
On munit
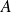 de la loi
de la loi
 définie par :
définie par :
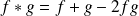 , et de la multiplication :
, et de la multiplication :
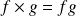 .
.
Question
Démontrer que
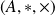 est un anneau commutatif.
est un anneau commutatif.
N'oubliez pas de démontrer que les lois sont internes.
Montrons d'abord que les lois sont internes. Soient
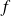 et
et
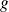 appartenant à
appartenant à
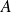 et
et
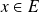 .
.
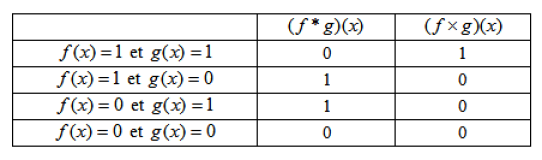
Donc :
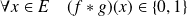 et
et
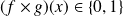 . Donc
. Donc
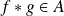 et
et
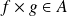 .
.
Donc les deux lois sont des lois de composition interne, commutatives de manière évidente.
Etudions l'associativité de la loi
 . Soient
. Soient
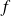 ,
,
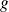 et
et
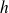 trois éléments de
trois éléments de
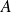 .
.On a :
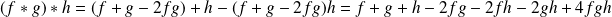 .
.Et :
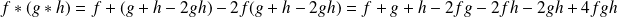 .
.Donc :
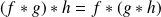 . Donc la loi
. Donc la loi
 est associative.
est associative.
La loi
 admet un élément neutre
admet un élément neutre
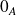 :
:
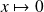 .
.En effet :
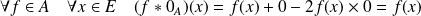 , donc
, donc
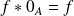 .
.Etudions l'inversibilité des éléments de
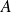 pour la loi
pour la loi
 .
.En remarquant que
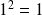 et
et
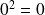 , on voit que :
, on voit que :
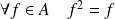 , et donc
, et donc
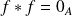 .
.Donc tout élément
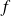 de
de
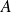 est symétrique de lui-même pour la loi
est symétrique de lui-même pour la loi
 .
.Il est évident que la multiplication est associative.
Etudions sa distributivité par rapport à la loi
 .
.Soient
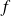 ,
,
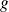 et
et
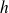 trois éléments de
trois éléments de
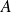 .
.On a :
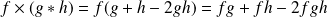 .
.Et :
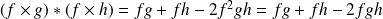 car
car
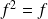 .
.Donc :
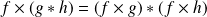 . Donc la loi
. Donc la loi
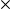 est distributive par rapport à la loi
est distributive par rapport à la loi
 .
.La loi
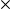 admet un élément neutre
admet un élément neutre
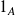 :
:
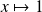 .
.
Conclusion :
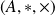 est un anneau commutatif.
est un anneau commutatif.
Question
En déduire que
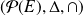 est un anneau commutatif.
est un anneau commutatif.
Pensez aux fonctions caractéristiques.
Soit
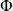 l'application qui à toute partie
l'application qui à toute partie
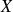 de
de
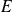 associe sa fonction caractéristique
associe sa fonction caractéristique
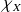 .
.
Or :
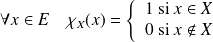 . Donc
. Donc
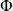 est une application de
est une application de
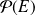 dans
dans
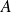 .
.
Elle est bijective car :
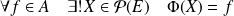 . C'est :
. C'est :
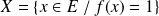 .
.
On a vu dans la séquence sur les ensembles que :
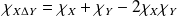 et
et
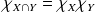 .
.
Donc pour toutes parties
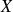 et
et
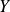 de
de
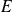 :
:
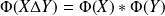 et
et
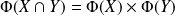 .
.
Donc
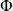 est un isomorphisme de
est un isomorphisme de
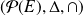 dans l'anneau commutatif
dans l'anneau commutatif
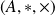 .
.
Conclusion :
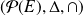 est un anneau commutatif.
est un anneau commutatif.





