Structure d'anneau
Définition :
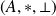 est un anneau si
est un anneau si
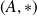 est un groupe commutatif et si la loi
est un groupe commutatif et si la loi
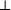 est interne, associative, distributive à gauche et à droite par rapport à la loi
est interne, associative, distributive à gauche et à droite par rapport à la loi
 et si elle a un élément neutre.
et si elle a un élément neutre.
L'ensemble des éléments inversibles (qui admettent un inverse pour la loi
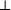 ) muni de la loi
) muni de la loi
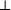 est un groupe.
est un groupe.
L'anneau est commutatif si la loi
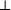 est commutative.
est commutative.
L'anneau est intègre si :
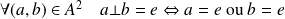 , où
, où
 est l'élément neutre de la loi
est l'élément neutre de la loi
 .
.
Exemple :
L'ensemble
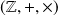 est un anneau commutatif intègre.
est un anneau commutatif intègre.
L'ensemble
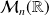 des matrices carrées d'ordre
des matrices carrées d'ordre
 , muni de l'addition et de la multiplication, est un anneau non commutatif et non intègre.
, muni de l'addition et de la multiplication, est un anneau non commutatif et non intègre.
Définition :
Une partie
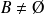 de
de
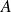 est un sous-anneau de
est un sous-anneau de
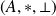 si la restriction des lois
si la restriction des lois
 et
et
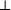 à
à
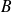 munit
munit
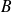 d'une structure d'anneau.
d'une structure d'anneau.
Une partie
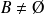 de
de
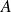 est un sous-anneau de
est un sous-anneau de
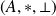 si et seulement si :
si et seulement si :
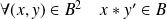 (où
(où
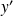 est le symétrique de
est le symétrique de
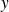 pour la loi
pour la loi
 ).
). 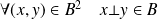 .
.L'élément neutre de la loi
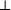 appartient à
appartient à
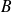 .
.
Définition :
Une partie
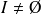 de
de
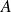 est un idéal à gauche de
est un idéal à gauche de
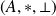 si
si
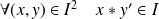 et
et
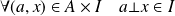 .
. Une partie
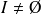 de
de
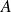 est un idéal à droite de
est un idéal à droite de
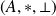 si
si
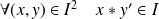 et
et
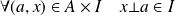 .
. L'idéal est bilatère s'il est idéal à gauche et à droite.
L'idéal est principal s'il est l'ensemble des multiples d'un unique élément
 .
. On le note
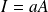 si c'est un idéal à gauche et
si c'est un idéal à gauche et
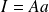 si c'est un idéal à droite.
si c'est un idéal à droite.
Exemple :
Tout idéal de
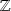 est principal, donc de la forme
est principal, donc de la forme
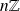 où
où
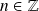 .
.
Dans la suite, on adoptera la notation
 et
et
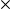 pour les deux lois.
pour les deux lois.
Fondamental :
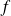 est un morphisme de l'anneau
est un morphisme de l'anneau
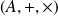 vers l'anneau
vers l'anneau
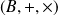 si :
si :
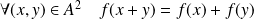 et
et
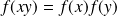 .
.
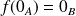 et
et
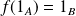 .
.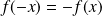 et, si
et, si
 est inversible,
est inversible,
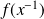 =
=
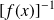 .
.L'image d'un sous-anneau de
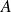 est un sous-anneau de
est un sous-anneau de
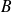 .
.L'image réciproque d'un sous-anneau de
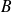 est un sous-anneau de
est un sous-anneau de
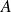 .
.L'image d'un idéal de
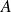 est un idéal de
est un idéal de
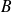 .
.L'image réciproque d'un idéal de
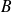 est un idéal de
est un idéal de
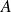 .
.





