Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Une grenouille monte un escalier de treize marches. Elle peut progresser soit en sautant d'une marche à la suivante, soit en sautant par dessus une marche. |  |
Question
De combien de façons distinctes peut-elle arriver au sommet de l'escalier ?
Codez la montée de l'escalier par la succession de sauts d'une marche (s) et de sauts de deux marches (S).
Une montée de l'escalier est une succession de sauts d'une marche (s) et de sauts de deux marches (S), par exemple : sSSsssSSs ou SSSSSSs.
Cependant, les nombres de sauts de deux marches et de sauts d'une marche ne sont pas indépendants puisqu'elle doit monter 13 marches.
Le nombre
de sauts de deux marches est un entier tel que :
, donc
.
Si
est le nombre de sauts de deux marches, le nombre de sauts d'une marche est
, donc le nombre total de sauts est
.
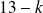Le nombre de montées avec
sauts de deux marches est donc le nombre de manières de choisir les places des
sauts de deux marches parmi ces
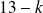sauts, donc
.
Donc le nombre total de montées de l'escalier est :
.
Conclusion : La grenouille a
façons distinctes de monter l'escalier.
Remarque :
Si l'escalier comporte
marches, on a :
.
