Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les traits du quadrillage ci-contre représente les rues d'une ville. Un promeneur (pressé !) veut se rendre de
Un chemin de
|  |
Question
Déterminer le nombre de chemins minimaux que peut emprunter le promeneur pour aller de
à
.
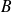Remarquez que tous les chemins minimaux ont la même longueur. En quoi diffèrent-ils ?
En prenant pour unité le côté d'un petit carré, tous les chemins minimaux ont pour longueur
:
vers la droite et
vers le haut.
Ils ne diffèrent que par l'ordre des mouvements vers la droite ou vers le haut.
Un chemin pourra par exemple être codé : DHHDDDHDDHHHDD.
Pour calculer le nombre de chemins minimaux, il suffit donc de choisir la place des
mouvements vers la droite parmi les
mouvements. Les autres seront les mouvements vers le haut.
Le nombre de chemins minimaux de
à
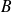est donc le nombre de tirages simultanés de
places parmi
, donc
.
Conclusion : Il y a
chemins minimaux de
à
.
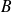Question
Déterminer le nombre de chemins minimaux qu'il peut emprunter s'il veut passer par
.
Le chemin de
à
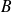est minimal si les chemins de
à
et de
à
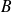sont minimaux.
Un chemin minimal de
à
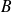passant par
est le raccordement d'un chemin minimal de
à
et d'un chemin minimal de
à
.
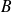Un chemin minimal de
à
comporte
mouvements vers la droite et
vers le haut. Il y en a donc
.
Un chemin minimal de
à
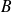comporte
mouvements vers la droite et
vers le haut. Il y en a donc
.
Les choix des chemins de
à
et de
à
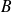sont indépendants.
Donc le nombre de chemins minimaux de
à
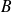passant par
est
.
Conclusion : Il y a
chemins minimaux de
à
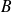qui passent par
.
