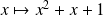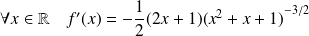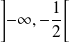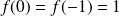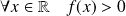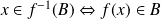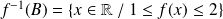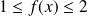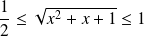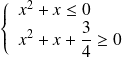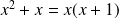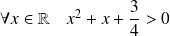Exo 12
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
la fonction définie par :
.
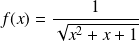Question
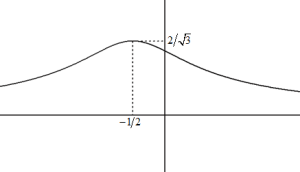
Déterminer l'ensemble de définition
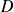de la fonction
et étudier ses variations.
Un réel
Or le discriminant est négatif. Donc :
La fonction
Donc
Et :
Donc
|  |
Conclusion : La fonction
est strictement croissante sur
et strictement décroissante sur
.
Question
La fonction
est-elle injective ? surjective de
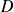dans
?
On peut remarquer que
Conclusion : La fonction
Et :
Conclusion : La fonction
|  |
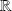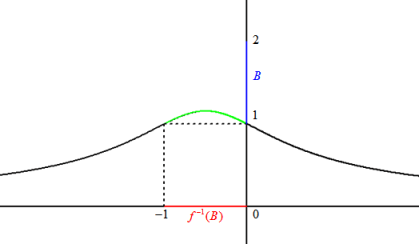
Question
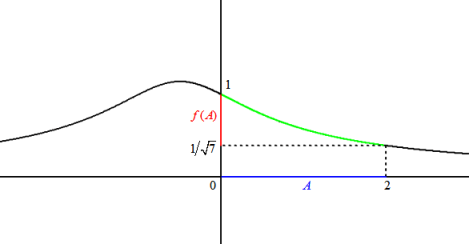
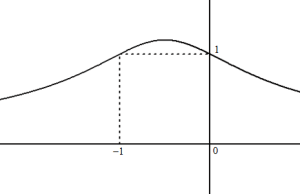
Déterminer l'image directe par
de
.
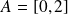Utilisez la définition :
.
La fonction
est strictement décroissante sur
, donc sur
.
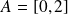Donc si
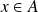, alors
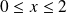, donc
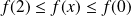, donc :
.
Donc
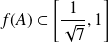. La continuité de
permet d'affirmer l'égalité.
On peut aussi la démontrer directement.
Soit
. On a
.
Le discriminant de cette équation est :
.
Or
. Donc
. Donc l'équation admet deux solutions réelles
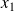et
.
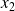Il s'agit maintenant de savoir si ces solutions appartiennent à
.
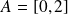Soit
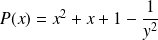. Donc
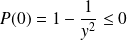et
.
Donc
. Donc :
.
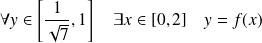Conclusion :
.
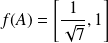