Exo 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Soient
et
deux ensembles non vides, et
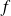une application de
dans
.
Démontrer que l'application
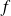est injective si et seulement si il existe une application
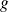de
dans
telle que
.
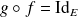A tout élément de
, on peut lui associer son antécédent s'il existe et s'il est unique.
On démontre successivement les deux implications.
On suppose qu'il existe une application
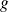de
dans
telle que
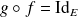.Soient
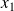et
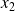deux éléments de
tels que
. Donc :
, donc:
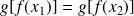, donc :
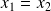.Donc l'application
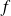est injective.
On suppose que l'application
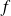est injective.Donc tout élément de
admet au plus un antécédent, donc s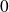oit
soit
antécédent.Soit
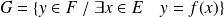l'ensemble des éléments de
qui ont un antécédent dans
.Soit
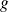l'application définie par :pour tout
,
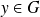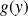est son unique antécédent.pour tout
,
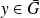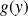est un élément fixé
de
.
Or pour tout
,
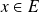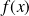appartient à
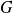, donc
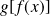est l'unique antécédent de
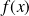, donc
.Donc il existe une application
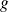de
dans
telle que
.
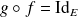Conclusion : L'application
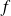est injective si et seulement si il existe une application
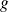de
dans
telle que
.
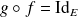