Injectivité
Définition :
Une application
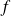 de
de
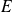 dans
dans
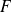 est injective si tout élément
est injective si tout élément
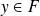 possède au plus un antécédent dans
possède au plus un antécédent dans
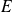 .
.
Pour tout élément
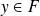 , l'équation
, l'équation
 possède au plus une solution dans
possède au plus une solution dans
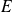 .
.
C'est équivalent à dire que deux éléments distincts de
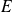 ne peuvent pas avoir la même image.
ne peuvent pas avoir la même image.
Méthode :
Pour démontrer qu'une application
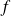 de
de
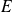 dans
dans
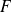 est injective, on suppose que
est injective, on suppose que
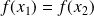 pour deux éléments quelconques
pour deux éléments quelconques
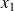 et
et
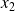 de
de
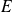 , et l'on démontre que
, et l'on démontre que
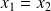 .
.
Fondamental :
Propriété :
Si
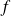 et
et
 sont deux applications injectives, leur composée
sont deux applications injectives, leur composée
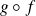 est injective.
est injective.





