Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
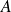et
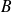deux parties d'un ensemble
.
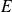Question
Démontrer que :
.
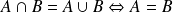Démontrez séparément les deux implications.
Commencez par l'implication la plus facile en supposant
.
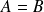Pour l'autre implication, démontrez successivement les deux inclusions
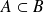et
.
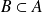Montrons que :
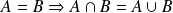. On suppose donc que :
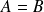. Donc :
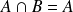et
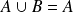. Donc :
.
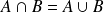Montrons que :
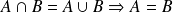. On suppose donc que :
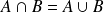.Or :
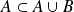, donc
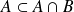. Or :
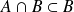. Donc :
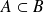.Et :
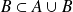, donc
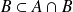. Or :
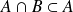. Donc :
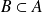.Donc :
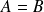puisque l'on a les deux inclusions.Conclusion :
.
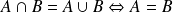