Calculer des réponses : algèbre
La requête (question) du calcul relationnel précédente (ou en SQL) précise bien ce qu'Alice demande. Cette question a un sens précis : une sémantique. Elle définit une réponse, un ensemble de n-uplets. Ce que la question ne dit pas c'est comment calculer la réponse. Pour le comment, on utilise l'algèbre relationnelle introduite par Codd, et que nous présentons à la troisième séquence de cette formation. Une étape importante consiste à transformer une question du calcul en une expression algébrique qui permet de calculer la réponse à cette question.
L'algèbre relationnelle consiste en un petit nombre d'opérations de base qui, appliquées à des relations, produisent de nouvelles relations. Ces opérations peuvent être composées pour construire des expressions algébriques de plus en plus complexes. Pour répondre à la question qui nous sert d'exemple, il nous faudra trois opérations, la jointure, la sélection et la projection, que nous composerons dans l'expression suivante de l'algèbre relationnelle :
EHB = πsalle,heure(πtitre(σacteur=“Humphrey Bogart”)(Film )) ⋈ Séance )
Nous pourrons suivre l'évaluation de cette expression algébrique dans la figure suivante. L'opération de sélection, dénotée σ, filtre une relation, ne gardant que les n-uplets satisfaisant une condition, ici acteur = “Humphrey Bogart”. L'opération de projection, dénotée π, permet aussi de filtrer de l'information d'une relation mais cette fois en éliminant des colonnes. L'opération peut-être la plus exotique de l'algèbre, la jointure, dénotée ⋈, combine des n-uplets de deux relations. D'autres opérations non illustrées ici permettent de faire l'union et la différence entre deux relations ou de renommer des attributs. La puissance de l'algèbre relationnelle tient de la possibilité de composer ces opérations. C'est ce que nous avons fait dans l'expression algébrique EHB qui permet d'évaluer la réponse à la question qHB.
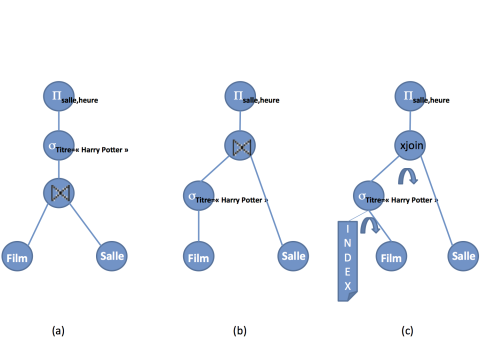
Notre présentation est rapide mais il est important que le lecteur comprenne l'intérêt de l'algèbre. Nous reviendrons là dessus plus en détail à la troisième séquence. En effet, il est relativement simple d'écrire un programme qui évalue la réponse à une question du calcul relationnel. Il est plus délicat d'obtenir un programme qui calcule cette réponse efficacement. L'algèbre relationnelle découpe le travail. Un programme particulier très efficace peut être utilisé pour chacune des opérations de l'algèbre ; le résultat est obtenu en composant ces programmes. L'efficacité provient notamment de ce que les opérations considèrent des ensembles de n-uplets plutôt que les n-uplets un à un.