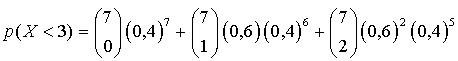Enoncé
5)
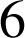étudiants sur
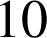d'une école d'ingénieurs sortent diplômés. On choisit au hasard
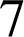étudiants sortants. Le nombre d'étudiants de cette école est assez important pour pouvoir considérer le choix des étudiants comme des tirages successifs avec remise. La probabilité qu'au moins
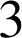étudiants parmi les
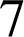soient diplômés est supérieure à
.
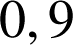Résultat
Correction
Explications
On choisit un étudiant. On appelle succès l'événement
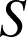: « l'étudiant est diplômé ».
.
On répète
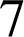fois la même expérience, les résultats étant indépendants d'après l'hypothèse. Soit
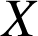la variable aléatoire qui compte le nombre de succès.
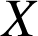suit la loi binomiale de paramètres 
.
La probabilité cherchée est 
.
Il y a deux méthodes pour calculer cette probabilité :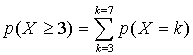 
ou 
.
La deuxième écriture est moins coûteuse en calculs.
