Monotonie d'une suite
Définition :
Par définition :
La suite
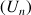est stationnaire à partir du rang
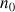si, pour tout
,
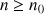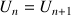
(on a alors
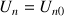pour tout
).
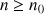La suite
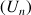est croissante à partir du rang
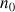si, pour tout
, 
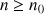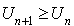.La suite
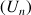est strictement croissante à partir du rang
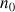si, pour tout
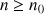, .La suite
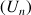est décroissante à partir du rang
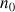si, pour tout
, 
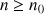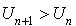.La suite
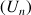est strictement décroissante à partir du rang
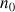si, pour tout
, 
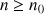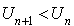.La suite
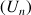est monotone si elle est croissante ou décroissante.
