Théorème
Soit
une fonction continue sur un intervalle
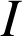et
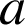un réel appartenant à
.
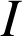La fonction 
est la primitive de
sur
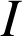qui s'annule en
.
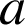Conséquence :
Toute fonction continue sur
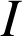admet des primitives sur
.
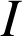