Calculer les intégrales suivantes :
1) ![]()
Soit
 la fonction définie sur
la fonction définie sur
 par :
par :
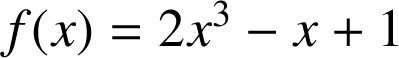 .
.
Comme
 est continue sur
est continue sur
 , elle y admet des primitives. L'une d'entre elles est la fonction
, elle y admet des primitives. L'une d'entre elles est la fonction
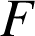 définie sur
définie sur
 par
par 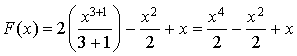 .
.
![]()
![]() .
.
2)![]()
Soit
 la fonction définie sur
la fonction définie sur
 par :
par : ![]() .
.
On pose
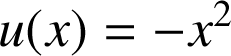 par conséquent
par conséquent
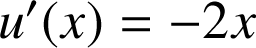 et on écrit
et on écrit
 sous la forme :
sous la forme : ![]() .
.
Or la fonction ![]() est la dérivée sur
est la dérivée sur
 de la fonction
de la fonction ![]() .
.
Comme
 est continue sur
est continue sur
 , elle y admet des primitives. L'une d'entre elles est la fonction
, elle y admet des primitives. L'une d'entre elles est la fonction
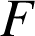 définie sur
définie sur
 par
par ![]() .
.
![]()
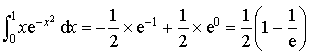
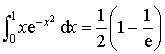 .
.
3) 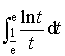
Soit
 la fonction définie sur
la fonction définie sur
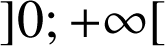 par
par ![]() .
.
On pose ![]() , par conséquent
, par conséquent ![]() , et on écrit
, et on écrit
 sous la forme :
sous la forme : ![]() .
.
Or la fonction ![]() est la dérivée sur
est la dérivée sur
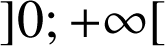 de la fonction
de la fonction ![]() .
.
Comme
 est continue sur
est continue sur
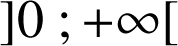 , elle y admet des primitives. L'une d'entre elles est la fonction
, elle y admet des primitives. L'une d'entre elles est la fonction
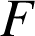 définie sur
définie sur
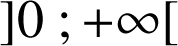 par
par ![]() .
.
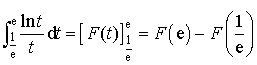
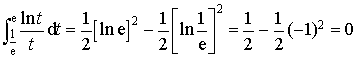
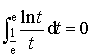 .
.
4) ![]()
Soit
 la fonction définie sur
la fonction définie sur
 par :
par : ![]() .
.
On pose
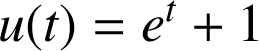 par conséquent
par conséquent
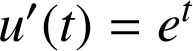 , et on écrit
, et on écrit
 sous la forme :
sous la forme : 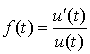 avec pour tout réel
avec pour tout réel
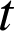 ,
, ![]() .
.
Or la fonction 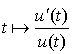 est la dérivée sur
est la dérivée sur
 de la fonction
de la fonction ![]() .
.
Comme
 est continue sur
est continue sur
 , elle y admet des primitives. L'une d'entre elles est la fonction
, elle y admet des primitives. L'une d'entre elles est la fonction
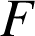 définie sur
définie sur
 par
par
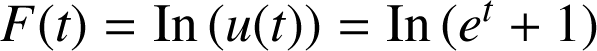 .
.
![]()
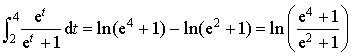
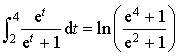 .
.






