Déterminer les primitives des fonctions suivantes sur les intervalles
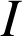 .
.
1) ![]() ,
, ![]() .
.
![]() .
.
 est définie et continue sur
est définie et continue sur
 donc
donc
 admet des primitives sur
admet des primitives sur
 .
.
 est de la forme
est de la forme
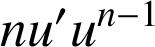 , avec
, avec
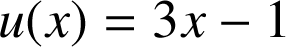 ,
,
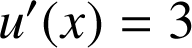 et
et
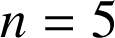 .
.
En effet ![]() .
.
Les primitives de
 sur
sur
 sont les fonctions
sont les fonctions
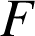 définies sur
définies sur
 par
par ![]() où
où
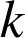 est un nombre réel.
est un nombre réel.
2) 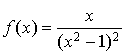 ,
, ![]() .
.
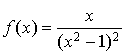 .
.
 est définie et continue sur
est définie et continue sur
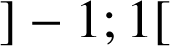 , donc
, donc
 admet des primitives sur
admet des primitives sur
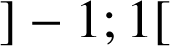 .
.
 est de la forme
est de la forme ![]() avec
avec
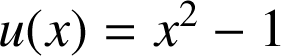 et
et
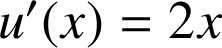 .
.
En effet 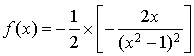 .
.
Les primitives de
 sur
sur
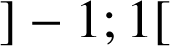 sont les fonctions
sont les fonctions
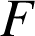 définies sur
définies sur
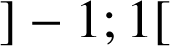 par
par ![]() où
où
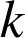 est un nombre réel.
est un nombre réel.
3) 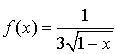 ,
, ![]() .
.
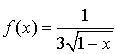 .
.
 est définie et continue sur
est définie et continue sur
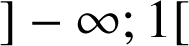 donc
donc
 admet des primitives sur
admet des primitives sur
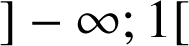 .
.
 est de la forme
est de la forme ![]() avec
avec ![]() et
et ![]() .
.
En effet 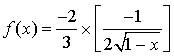 .
.
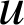 est strictement positive sur
est strictement positive sur
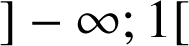 , donc les primitives de
, donc les primitives de
 sur
sur
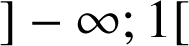 sont les fonctions
sont les fonctions
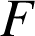 définies sur
définies sur
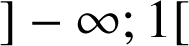 par
par ![]() où
où
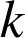 est un nombre réel.
est un nombre réel.
4) ![]() ,
, ![]() .
.
![]() .
.
 est définie et continue sur
est définie et continue sur
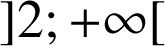 donc
donc
 admet des primitives sur
admet des primitives sur
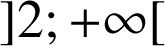 .
.
Nous remarquons que
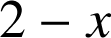 est strictement négatif pour
est strictement négatif pour
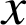 appartenant à
appartenant à
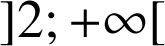 .
.
 est de la forme
est de la forme ![]() avec
avec ![]() et
et ![]() .
.
En effet 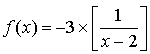 .
.
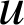 est strictement positive sur
est strictement positive sur
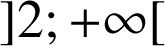 , donc les primitives de
, donc les primitives de
 sur
sur
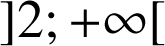 sont les fonctions
sont les fonctions
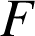 définies sur
définies sur
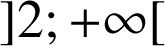 par
par ![]() où
où
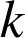 est un nombre réel.
est un nombre réel.
5) ![]() ,
, ![]() .
.
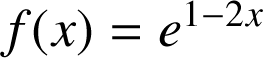 .
.
 est définie et continue sur
est définie et continue sur
 donc
donc
 admet des primitives sur
admet des primitives sur
 .
.
 est de la forme
est de la forme
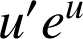 avec
avec
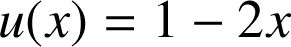 et
et
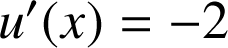 .
.
En effet ![]() . Les primitives de
. Les primitives de
 sur
sur
 sont les fonctions
sont les fonctions
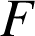 définies sur
définies sur
 par
par ![]() où
où
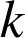 est un nombre réel.
est un nombre réel.
6) ![]() ,
, ![]() .
.
Exprimer
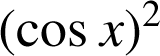 en fonction de
en fonction de
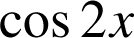 .
.
![]() .
.
 est définie et continue sur
est définie et continue sur
 donc
donc
 admet des primitives sur
admet des primitives sur
 .
.
Pour tout
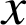 réel,
réel, ![]() .
.
La fonction ![]() est de la forme
est de la forme
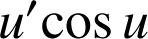 avec
avec
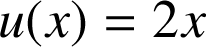 et
et
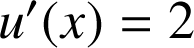 .
.
En effet, ![]() .
.
Les primitives de
 sur
sur
 sont les fonctions
sont les fonctions
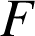 définies sur
définies sur
 par
par ![]() où
où
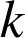 est un nombre réel.
est un nombre réel.
7) ![]() ,
, ![]() .
.
Faire apparaître
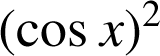 .
.
![]() .
.
 est définie et continue sur
est définie et continue sur
 donc
donc
 admet des primitives sur
admet des primitives sur
 .
.
Pour tout
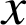 réel,
réel,
La fonction ![]() est de la forme
est de la forme
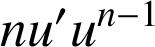 avec
avec
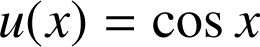 ,
,
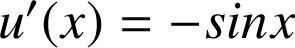 et
et
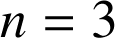 .
.
En effet ![]() .
.
Les primitives de
 sur
sur
 sont les fonctions
sont les fonctions
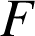 définies sur
définies sur
 par
par ![]() où
où
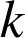 est un nombre réel.
est un nombre réel.
8) ![]() ,
, 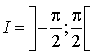 .
.
![]() .
.
 est définie et continue sur
est définie et continue sur 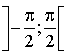 donc
donc
 admet des primitives sur
admet des primitives sur 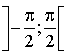 .
.
![]() .
.
 est de la forme
est de la forme ![]() avec
avec
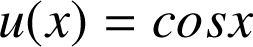 et
et
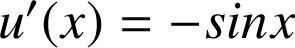 .
.
En effet 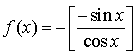 .
.
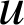 est strictement positive sur
est strictement positive sur 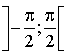 , donc les primitives de
, donc les primitives de
 sur
sur 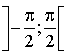 sont les fonctions
sont les fonctions
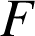 définies sur
définies sur 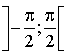 par
par ![]() où
où
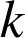 est un nombre réel.
est un nombre réel.






