Enoncé
2) Soit
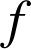 la fonction définie par
la fonction définie par 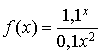 avec
avec ![]() .
.
Résultat
Correction
Explications
A.
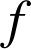 est définie pour tout
est définie pour tout ![]()
Sachant que pour
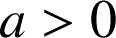 , la fonction
, la fonction ![]() est définie sur
est définie sur
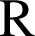 , seul le réel
, seul le réel
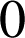 qui annule le dénominateur
qui annule le dénominateur
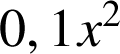 est à rejeter.
est à rejeter.
B. ![]()
En posant ![]() comme
comme ![]() si
si ![]() , alors
, alors ![]() et
et 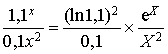 .
.
Or 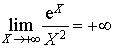 (référence du cours :
(référence du cours : ![]() ) et
) et 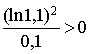 donc
donc ![]() .
.
C. Pour ![]() ,
,
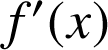 a le même signe que
a le même signe que ![]()
Sachant que la fonction ![]() est dérivable sur
est dérivable sur
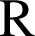 donc sur
donc sur
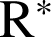 et que la fonction
et que la fonction ![]() est dérivable et non nulle sur
est dérivable et non nulle sur
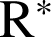 , la fonction
, la fonction
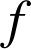 est dérivable sur
est dérivable sur
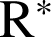 et pour tout
et pour tout
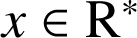 ,
,
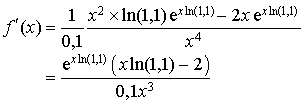
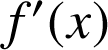 est donc du signe de
est donc du signe de ![]() uniquement si
uniquement si ![]() et non pour tout
et non pour tout
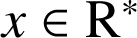 .
.
D. La fonction
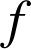 admet sur
admet sur
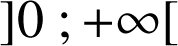 un minimum égal à
un minimum égal à ![]()
Sur
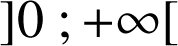 ,
,
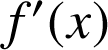 est du signe de
est du signe de ![]() d'où les variations de
d'où les variations de
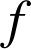 sur
sur
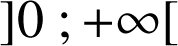 .
.
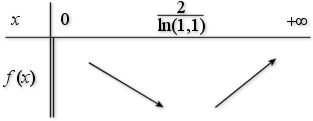
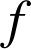 admet donc un minimum égal à
admet donc un minimum égal à 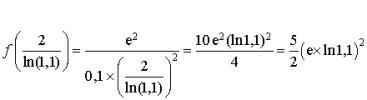 .
.
![]() donc la réponse est fausse.
donc la réponse est fausse.