Enoncé
1) Soit
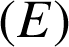 l'équation
l'équation
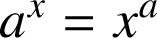 avec a paramètre strictement positif.
avec a paramètre strictement positif.
Dans
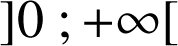 , l'ensemble
, l'ensemble
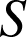 des solutions de
des solutions de
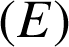 vérifie :
vérifie :
Résultat
Correction
Explications
A. Pour
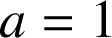 ,
, ![]()
Dans
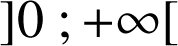 , pour
, pour
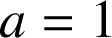 ,
, ![]()
![]() donc
donc
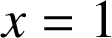 est la seule solution de
est la seule solution de
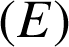 .
.
B. Pour
 ,
, ![]()
Le réel
 est solution donc
est solution donc
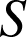 n'est pas égal à l'ensemble vide.
n'est pas égal à l'ensemble vide.
C. Pour
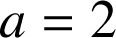 ,
,
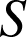 admet deux éléments
admet deux éléments
Pour
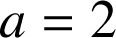 , dans
, dans
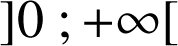 ,
, ![]()
L'étude des variations de la fonction
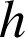 définie par
définie par ![]() donne :
donne :
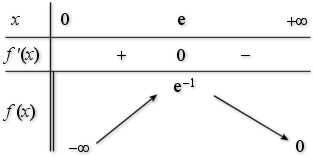
![]() d'où d'après le tableau de variation de
d'où d'après le tableau de variation de
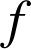 , l'équation
, l'équation ![]() admet (conséquence du théorème des valeurs intermédiaires), une solution unique dans
admet (conséquence du théorème des valeurs intermédiaires), une solution unique dans ![]() et une solution unique dans
et une solution unique dans ![]() donc
donc
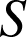 admet deux éléments.
admet deux éléments.
D. Pour
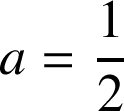 ,
,
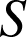 admet un seul élément
admet un seul élément
Pour
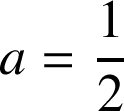 , dans
, dans
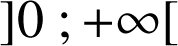 ,
, ![]() (voir démarche au C).
(voir démarche au C).
D'après l'étude des variations de la fonction ![]() (voir proposition C),
(voir proposition C), ![]() donc l'équation
donc l'équation ![]() admet une seule solution dans et aucune dans
admet une seule solution dans et aucune dans ![]() . L'ensemble
. L'ensemble
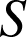 a donc un seul élément qui est
a donc un seul élément qui est
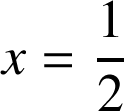 .
.