Enoncé
3) La fonction
 est définie par
est définie par ![]() avec
avec
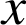 réel.
réel.
Résultat
Correction
Explications
A. Les équations ![]() et
et
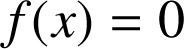 ont une seule solution dans
ont une seule solution dans
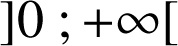
Soit
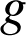 la fonction définie par
la fonction définie par ![]() ;
;
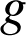 est la somme de deux fonctions strictement croissantes et continues sur
est la somme de deux fonctions strictement croissantes et continues sur
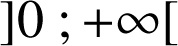 ,
, ![]() et
et ![]() ; d'après le théorème des valeurs intermédiaires l'équation
; d'après le théorème des valeurs intermédiaires l'équation
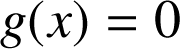 admet une seule solution dans
admet une seule solution dans
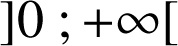 .
.
L'équation
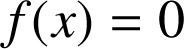 est équivalente à l'équation
est équivalente à l'équation ![]() dans
dans
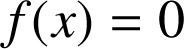 ,d'où elle n'admet qu'une seule solution dans
,d'où elle n'admet qu'une seule solution dans
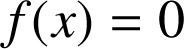 .
.
B. ![]() et
et ![]()
![]()
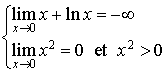
Par contre ![]() .
.
![]() et
et ![]() ,
, ![]() (pour
(pour ![]() ,
, ![]() ).
).
C. Pour tout ![]() ,
, ![]()
Les fonctions ![]() et
et ![]() sont dérivables sur
sont dérivables sur
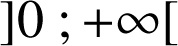 avec
avec
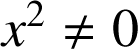 donc
donc
 est dérivable sur
est dérivable sur
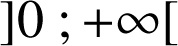 et
et 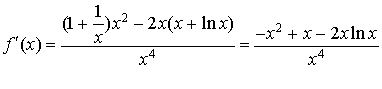 , soit
, soit ![]() .
.
D. Une primitive de
 sur
sur
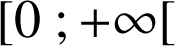 est
est ![]()
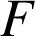 est la somme de trois fonctions dérivables sur
est la somme de trois fonctions dérivables sur
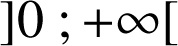 et pour tout
et pour tout ![]() ,
, ![]() .
.