Enoncé
2) La fonction
 est définie par
est définie par 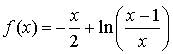 avec
avec
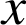 réel.
réel.
 est sa représentation graphique dans un repère orthonormal
est sa représentation graphique dans un repère orthonormal ![]() .
.
Résultat
Correction
Explications
A.
 n'est pas définie pour
n'est pas définie pour ![]()
Pour ![]() ,
,
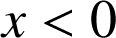 et
et
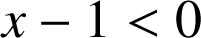 d'où le quotient
d'où le quotient ![]() et
et 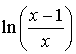 est défini.
est défini.
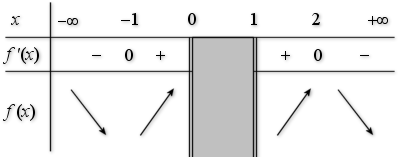
B. La courbe
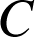 a des tangentes horizontales aux points d'abscisse
a des tangentes horizontales aux points d'abscisse
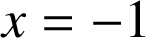 sur
sur ![]() et
et
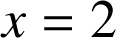 sur
sur ![]()
Sur
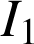 et sur
et sur
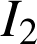 la fonction
la fonction ![]() est dérivable (fonction affine) et la fonction
est dérivable (fonction affine) et la fonction ![]() est dérivable (composée de la fonction rationnelle
est dérivable (composée de la fonction rationnelle ![]() et de la fonction
et de la fonction
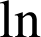 ).
).
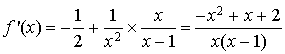
![]()
Le polynôme
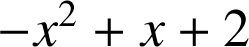 admet pour racines
admet pour racines
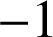 et
et
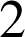 donc la dérivée s'annule en
donc la dérivée s'annule en
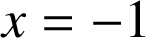 sur
sur ![]() et en
et en
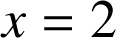 sur
sur ![]() .
.
C. La fonction
 est décroissante sur
est décroissante sur
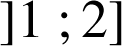
Pour ![]() ,
, 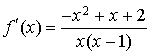 d'où
d'où ![]() (
(
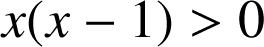 et le polynôme
et le polynôme
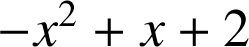 est positif entre ses racines soit sur
est positif entre ses racines soit sur
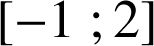 ) ;
) ;
 est donc croissante sur
est donc croissante sur
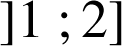 .
.
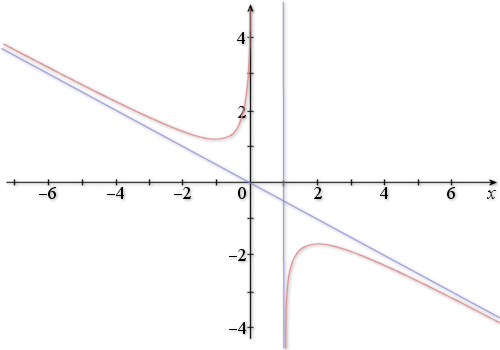
D. La courbe
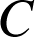 admet une asymptote d'équation
admet une asymptote d'équation
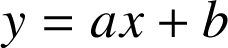
La droite d'équation ![]() est asymptote à
est asymptote à
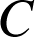 en
en
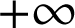 et en
et en
 ;
;
![]() avec
avec ![]() ,
, ![]() et
et ![]() (
(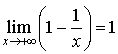 ,
, 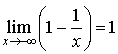 et
et ![]() ).
).