Enoncé
4) La fonction
 est définie par
est définie par ![]() avec
avec
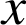 réel.
réel.
Résultat
Correction
Explications
A. La fonction
 est définie pour tout
est définie pour tout ![]()
La fonction
 n'est pas définie pour
n'est pas définie pour
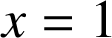 qui annule le dénominateur.
qui annule le dénominateur.
B. La fonction
 est décroissante sur
est décroissante sur ![]()
La fonction ![]() est dérivable et non nulle sur
est dérivable et non nulle sur ![]() donc
donc
 est dérivable sur
est dérivable sur ![]() et
et 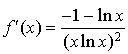
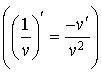 .
.
![]() , donc sur
, donc sur ![]() ,
, ![]() .
.
C. Sur ![]() , une primitive de
, une primitive de
 est
est
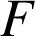 définie par
définie par ![]()
La fonction ![]() est dérivable et non nulle sur
est dérivable et non nulle sur ![]() donc la fonction
donc la fonction
 est dérivable sur
est dérivable sur ![]() et elle admet des primitives sur
et elle admet des primitives sur ![]() ;
;
 est de la forme
est de la forme ![]() avec
avec ![]() et
et
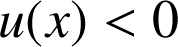 sur
sur ![]() donc
donc ![]() .
.
D. L'équation ![]() admet une seule solution dans
admet une seule solution dans
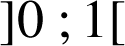
Pour tout ![]() ,
, ![]() d'où
d'où
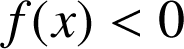 ; le réel
; le réel ![]() est strictement positif donc l'équation
est strictement positif donc l'équation ![]() n'a pas de solution dans
n'a pas de solution dans
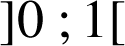 .
.
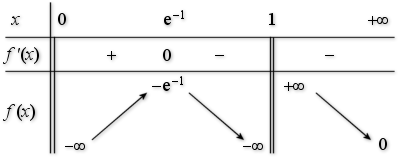
REMARQUE : l'étude des variations de
 prouve que, sur
prouve que, sur
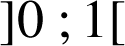 ,
,
 admet pour maximum le réel
admet pour maximum le réel
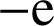 ; or
; or ![]() .
.