Enoncé
1) Soit
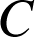 la courbe d'équation
la courbe d'équation ![]() dans un repère orthonormal
dans un repère orthonormal ![]() représentative d'une fonction
représentative d'une fonction
 .
.
Résultat
Correction
Explications
A. La fonction
 est définie pour tout
est définie pour tout
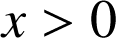
La condition
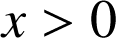 est nécessaire mais ne suffit pas pour le dénominateur qui ne doit pas s'annuler d'où
est nécessaire mais ne suffit pas pour le dénominateur qui ne doit pas s'annuler d'où
 n'est pas définie pour
n'est pas définie pour ![]() .
.
B. ![]()
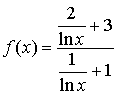 pour
pour ![]() , d'où
, d'où ![]() (
(![]() ).
).
Autre méthode : en posant ![]() , si
, si ![]() alors
alors ![]() et
et ![]() .
.
C. La courbe
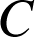 admet pour asymptote la droite d'équation
admet pour asymptote la droite d'équation ![]()
 n'est pas définie en
n'est pas définie en ![]() et
et 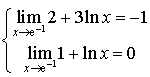 ,
,
d'où 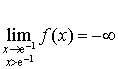
![]() et
et 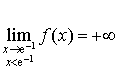
![]() .
.
D. La courbe
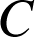 admet pour asymptote la droite d'équation
admet pour asymptote la droite d'équation
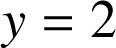
A l'aide de l'écriture 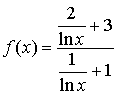 , on en déduit que
, on en déduit que ![]() (
(![]() ) ou à l'aide du changement de variable
) ou à l'aide du changement de variable ![]() on en déduit que
on en déduit que ![]() . C'est la droite d'équation
. C'est la droite d'équation
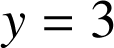 qui est asymptote à la courbe
qui est asymptote à la courbe
 en
en
 .
.
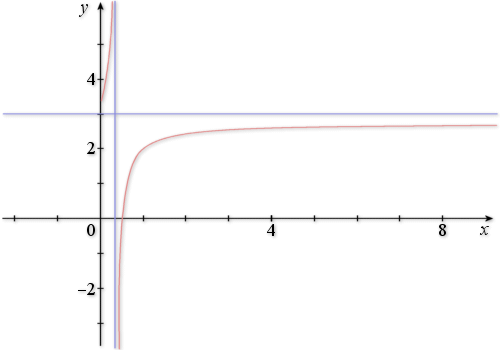
Courbe C représentative de f